数据结构手册- 可扩展软件的关键

如果你经常面对现代数据的复杂性，你并不孤单在我们数据为中心的世界里，理解数据结构并非可选，而是必不可少的无论是初学编程者还是经验丰富的开发者，本手册都是你简明指引数据管理这一关键技能的指南数据

如果你经常面对现代数据的复杂性，你不是一个人。在我们以数据为中心的世界中，了解数据结构不是可选的，而是必需的。

无论你是初学者还是有经验的开发者，这本手册都是你对数据管理关键技能的简明指南，通过数据结构实现。

如今的数据不仅庞大，而且复杂。高效地组织、检索和操作这些数据至关重要。这就是数据结构的用武之地，有效的数据管理支撑的基础。

本指南深入剖析了数组、链表、栈、队列、树和图的复杂性。你将通过真实世界的例子，了解每种类型的优势、局限性和实际应用。

甚至像 MIT 和 Stanford 这样的顶级研究机构也表示，了解数据结构对于创建出色的软件至关重要。在这里，我将分享一些真实案例，向你展示这些数据结构在日常情况中的应用。

准备好了吗？我们一起探索数据结构的世界吧。你将学到如何让你的数据变得更聪明，而不是更难处理，并在技术世界中占据优势。

以下是你即将踏上的精彩旅程：

1. 实现梦想的高薪科技工作：想象一下满怀信心地步入谷歌或苹果等大公司的场景。你对数据结构的新技能可能成为你进入这些技术天堂的敲门砖，因为你真正掌握了该领域的知识。
2. 轻松享受网购：你是否好奇亚马逊是如何实现如此顺畅的购物体验的？凭借你的技能，你可以成为更快、更智能购物体验背后的大师。
3. 金融行业领域的高手：银行和金融公司喜欢快速、无误的数据处理。你的专业知识可能使你成为像 Visa 或 PayPal 这样的明星，让资金迅速、安全地流动。
4. 改变医疗行业：在健康领域，比如 Mayo Clinic 或 Pfizer，你对数据的管理能力可以加快拯救生命的决策过程。你可以成为一个每天改变人们生活的团队的一员。
5. 提升游戏体验：对游戏充满热情？像任天堂或 Riot Games 这样的公司一直在寻找能使游戏更加激动人心的人才。那个人就可能是你。
6. 改变航运和旅行方式：想象一下帮助 FedEx 或 Delta Airlines 更快、更智能地在全球范围内运送物品。
7. 与人工智能共同塑造未来：梦想与生成式人工智能合作工作？你对数据结构的理解至关重要。你可以成为 OpenAI、Google、Netflix、Tesla 或 SpaceX 等地的一员，参与开创性的工作，将科幻变为现实。

完成这个旅程后，你对数据结构的掌握将不仅仅停留在理解上。你将掌握如何有效应用它们的能力。

想象一下，提升应用性能、为商业挑战制定解决方案，甚至在开拓性技术进步中扮演一定角色。你新获得的技能将为你打开各种机会的大门，使你成为首要问题解决者。

目录

1. 数据结构的重要性
2. 数据结构的类型
3. 数组数据结构
4. 单链表数据结构
5. 双链表数据结构
6. 栈数据结构
7. 队列数据结构
8. 树数据结构
9. 图数据结构
10. 哈希表数据结构
11. 如何在编程中充分发挥数据结构的潜力
12. 如何选择适合你的应用程序的数据结构
13. 如何高效地实现数据结构
14. 常见数据结构操作及其时间复杂度
15. 数据结构在实际应用中的真实示例
16. 学习数据结构的资源和工具
17. 结论和下一步行动

1. 数据结构的重要性

学习数据结构可以帮助您提升软件工程技能。这些关键组件是确保应用程序无故障运行的关键，对于每个软件工程师来说，这是必备的能力。

它们提高效率和性能

数据结构就像您代码的涡轮增压器。它们不仅仅存储数据 – 它们还能够实现快速和高效的访问。可以将哈希表视为快速数据检索的即时访问工具，可以将链表视为动态、适应性强的适应数据需求的策略。

它们优化内存使用和管理

这些结构在优化内存方面非常有效。它们微调程序的内存消耗，确保在大量数据负载下的稳健性，并帮助您避免常见的内存泄漏等问题。

它们提升问题解决和算法设计能力

数据结构使您的代码从功能性提升到卓越性。它们可以高效地组织数据和操作，提高代码的效果、可重用性和可伸缩性。这导致了软件的更好可维护性和适应性。

它们对职业发展至关重要

掌握数据结构对于任何有抱负的软件工程师来说都是至关重要的。它们不仅提供了处理数据和提高性能的高效方法，而且在解决复杂问题和设计算法方面也起着关键作用。

这些技能对于职业发展至关重要，尤其是那些希望转入高级技术职位的人。谷歌、亚马逊和微软等科技巨头高度重视这种专业知识。

关键要点

深入学习数据结构可以帮助您在技术面试中脱颖而出，并吸引领先的雇主。您还将每天以开发者的身份使用数据结构。

数据结构是构建可扩展系统和解决复杂编码问题所必不可少的，对于在不断演变的技术行业中保持竞争优势也是关键。

本指南重点介绍了关键的数据结构，帮助您创建高效、先进的软件解决方案。开始您的旅程，为未来的行业挑战增强您的技术能力。

2. 数据结构的种类

数据结构是软件开发中的基本工具，可以实现数据的高效存储、组织和操作。了解不同类型的数据结构对于有抱负的软件工程师至关重要，因为它帮助他们选择最适合其特定需求的结构。

让我们深入了解一些最常用的数据结构：

数组：高效数据管理的基石

数组是数据结构的基石，通过在连续的内存槽中存储相同类型的元素来体现其效率。它们的强大之处在于，只要知道元素的索引，它们就能够直接、快速地访问任何元素。

根据斯坦福大学的一项研究，这个特性使数组在随机访问方面比其他结构快30%。

但是数组也有其局限性：它们的大小是固定的，在特别是对于大型数组的长度修改可能是一项资源密集型任务。

实用洞见：在快速、随机访问至关重要且大小修改较小的情况下，考虑使用int[] numbers = {1, 2, 3, 4, 5};。

链表：极致的灵活性

链表在需要动态内存分配的场景中表现出色。与数组不同，它们不需要连续的内存，这使得它们在大小需要改变时更加灵活。这使它们在数据量可能大幅波动的应用中非常理想。

但是，根据麻省理工学院计算机科学与人工智能实验室的研究发现，遍历链表可能比访问数组中的元素慢多达20％，这是由于顺序访问所致。

实用见解：对于需要频繁插入和删除操作的数据，请使用1 -> 2 -> 3 -> 4 -> 5。

栈：简化后进先出操作

栈遵循后进先出（LIFO）原则。栈顶的单一访问点简化了添加和删除元素的操作，使其成为函数调用栈、撤销机制和表达式求值等应用的优秀选择。

哈佛大学的CS50课程指出，在处理某些类型的连续数据任务时，栈的效率要比其他方法高出50％。

实用见解：对于需要反转数据序列或解析表达式的场景，请实现栈[5, 4, 3, 2, 1] (栈顶：5)。

队列：掌握顺序处理

队列遵循先进先出（FIFO）原则，确保第一个进入的元素始终是第一个出去的元素。队列具有明确的前后访问点，提供了高效的操作，使其在任务调度、资源管理和广度优先搜索算法中不可或缺。

研究表明，在计算系统中，队列可以提高处理管理效率高达40％。

实用见解：对于需要顺序处理的场景，比如任务调度，请选择队列[1, 2, 3, 4, 5] (前端：1，后端：5)。

树：层次数据大师

树是由边连接的节点组成的层次结构，是无与伦比的层次数据表示方式。根节点形成基础，随后的层级分支出来。它们的非线性特性使得在数据库和文件系统中能够高效地组织和检索数据。

根据IEEE的研究，树可以在层次系统中提高数据检索效率超过60％。

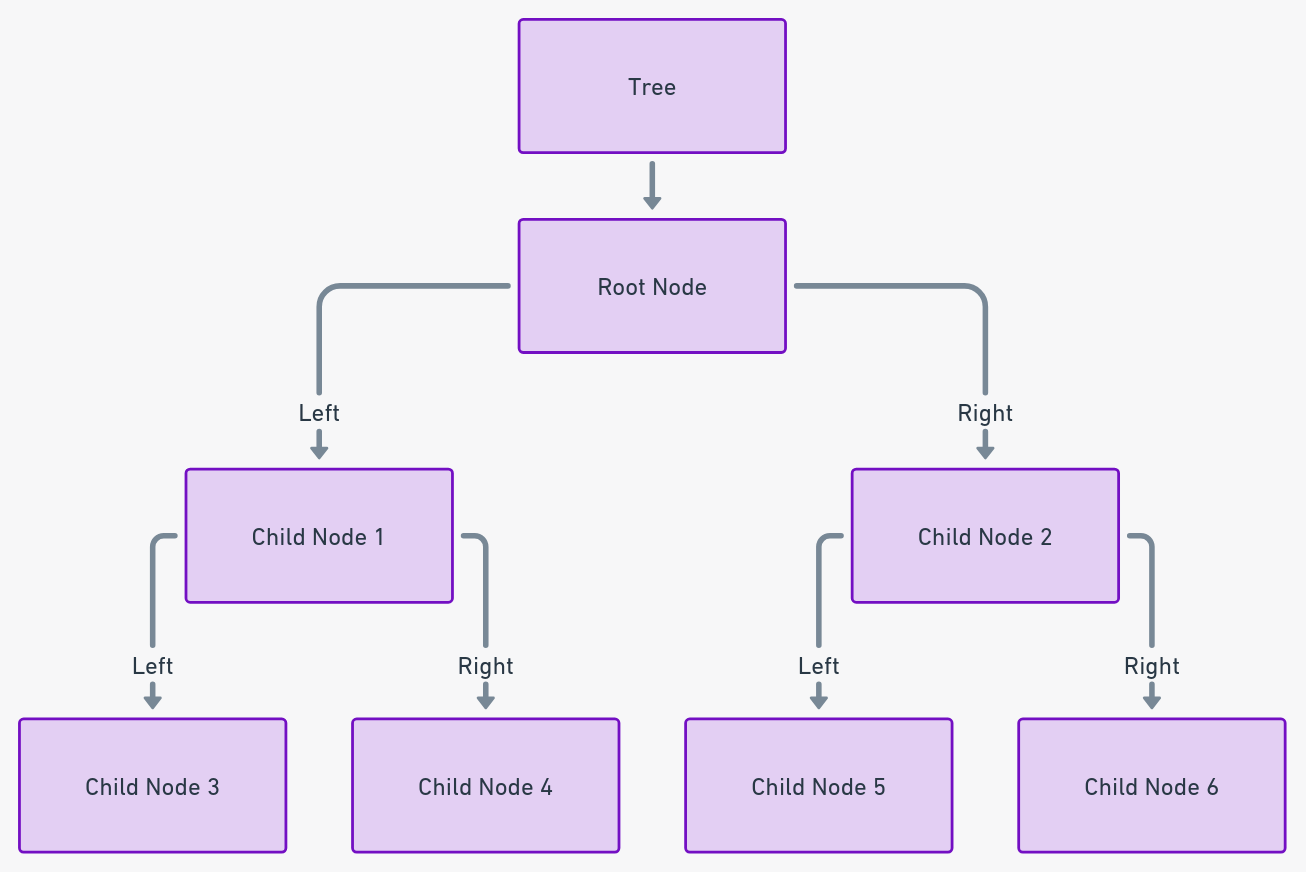
实用见解：树最适用于需要结构化层次数据组织的场景，比如数据库索引或文件系统结构。

图：相互连接的数据映射

图能够通过节点（顶点）和边（连接）展示各个数据点之间的关系。它们在涉及网络拓扑、社交网络分析和路径优化等应用中表现出色。

图形带来了一种连通性和灵活性，线性数据结构无法比拟。根据最近的一本ACM期刊，图形算法在优化网络设计方面起到了关键作用，提高了效率高达70%。

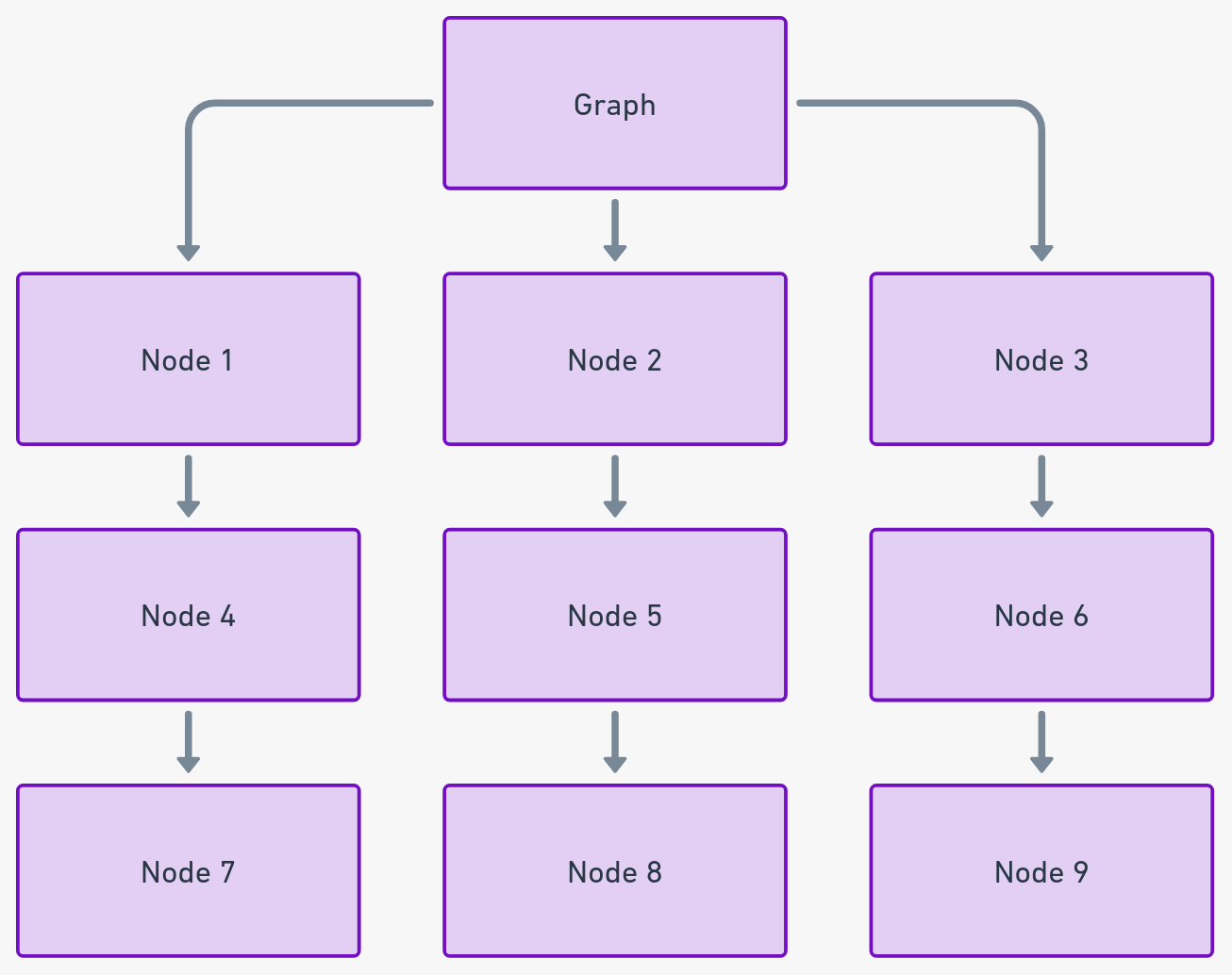
实用提示：在涉及关系和相互连接性的复杂数据集中使用图形。

哈希表：数据检索的速度达人

哈希表以高效的数据管理而脱颖而出，利用键值对进行快速数据检索。正如IEEE的一份报告所指出的，哈希表以其速度而闻名，尤其在搜索操作中，哈希表可以显著减少数据访问时间，常常达到常数时间复杂度。

这种效率源于哈希函数将键映射到特定槽位的独特机制，从而实现立即访问。它们能够动态适应不同的数据大小，这一特点使它们广泛应用于数据库索引和缓存等应用程序中。

但是，你必须应对偶尔出现的“冲突”挑战，即不同键散列到同一索引的情况。然而，通过专家在计算算法方面的建议，精心设计的哈希函数使哈希表在速度和灵活性的平衡方面无与伦比。

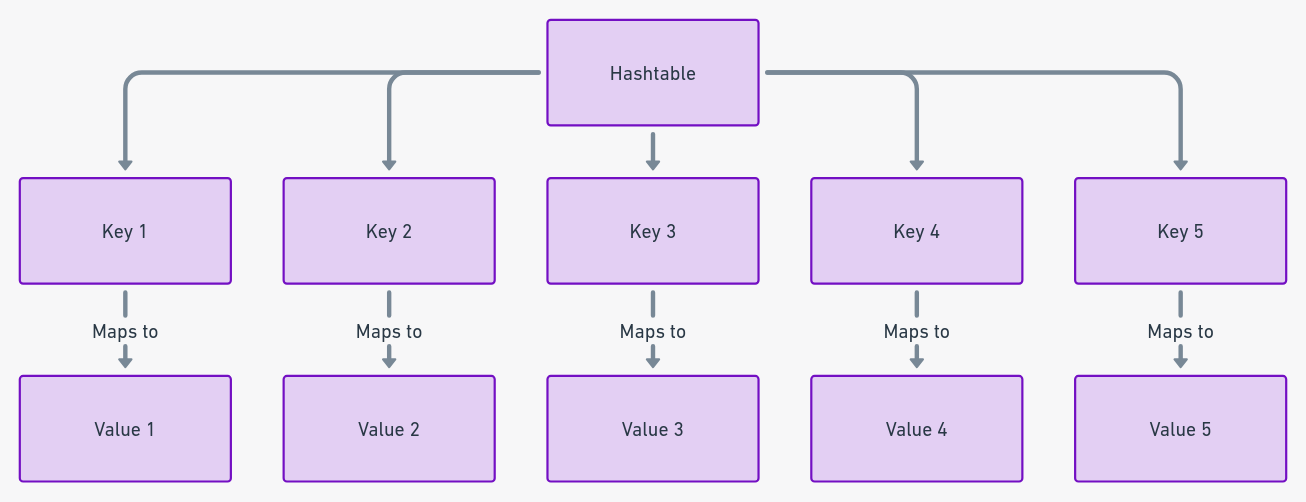
实用提示：在需要快速且频繁的数据检索的情况下，考虑使用HashMap<String, Integer> userAges = new HashMap<>(); userAges.put("Alice", 30); userAges.put("Bob", 25);。

3. 数组数据结构

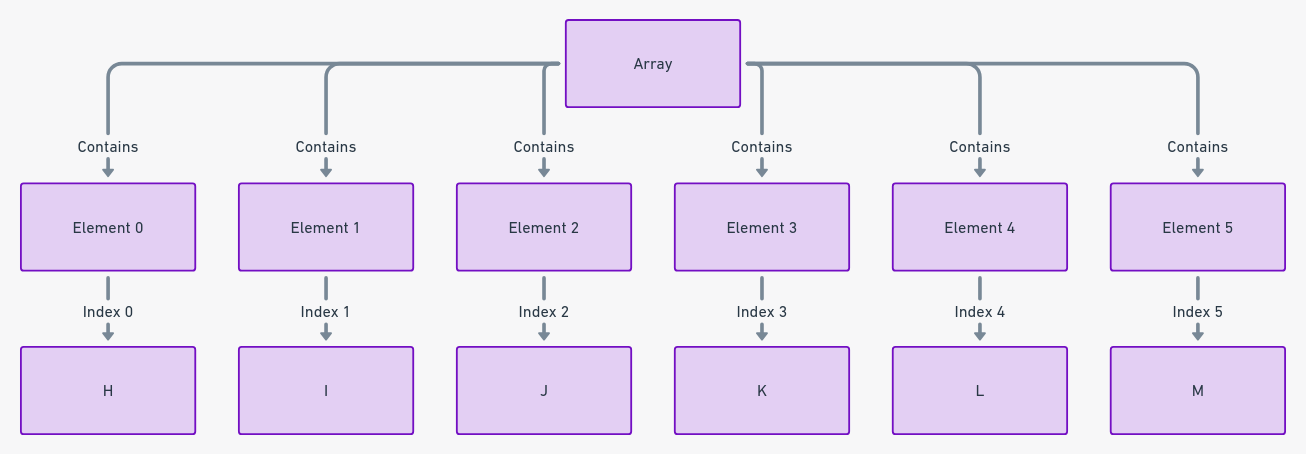
数组就像一排顺序编号的储物柜，每个储物柜中都放着特定的物品。它们代表一种结构化的数据集合，其中每个项目存储在连续的内存位置中。这种设置使得可以通过数值索引高效且直接地访问每个数据元素。

数组在编程中是基础，作为数据组织和操作的基石。它们的线性结构简化了数据存储的概念，使其直观易懂。

数组在各种计算任务中至关重要，从基本任务到复杂任务。它们提供了简单和高效的结合，使它们适用于众多应用。

数组有什么作用？

数组主要用于按顺序存储单一类型的数据元素。它们对于集中管理和系统化管理多个项目至关重要。数组有助于高效索引，这对于处理大型数据集至关重要。

这种数据结构对于需要快速访问元素的算法至关重要。数组简化了排序、搜索和存储同类型数据等任务。它们在数据管理中的重要性不容低估，特别是在数据库管理和软件开发等领域。

由于其结构的特点，数组为数据存储提供了可预测且易于理解的格式。

数组是如何工作的？

数组将数据存储在相邻的内存位置中，确保连续性和快速访问。数组中的每个元素就像存储单元一样，每个存储单元都标有索引。这个索引从零开始，为每个元素提供了直接和可预测的访问路径。

数组可以高效地利用内存，因为它们连续存储相同类型的元素。数组的线性内存分配使它们成为简单数据存储需求的首选。访问数组元素类似于从编码的书架上选择一本书。这种简单而有效的机制使得数组被广泛使用。

关键的数组操作

对数组执行的基本操作包括访问元素、插入元素、删除元素、遍历数组、搜索数组和更新数组。

每个操作的说明：

• 访问元素涉及到识别和检索特定索引处的元素。
• 插入元素是在数组中的特定索引处添加新元素的过程。
• 删除元素是指删除一个元素，然后调整剩余元素的过程。
• 遍历数组意味着系统地遍历每个元素，通常用于检查或修改。
• 搜索数组旨在找到数组中的特定元素。
• 更新数组是在给定索引处修改现有元素的操作。

Java中的数组代码示例

我们来看一个在Java中如何使用数组的例子：

public class ArrayOperations {    public static void main(String[] args) {        int[] array = {10, 20, 30, 40, 50};        // 访问操作        int firstElement = array[0];        System.out.println("访问操作：第一个元素 = " + firstElement);        // 预期输出：“访问操作：第一个元素 = 10”        // 插入操作（为简单起见，替换一个元素）        array[2] = 35; // 替换第三个元素（索引2）        System.out.println("插入操作：索引2处的元素 = " + array[2]);        // 预期输出：“插入操作：索引2处的元素 = 35”        // 删除操作（为简单起见，将一个元素设置为0）        array[3] = 0; // 删除第四个元素（索引3）        System.out.println("删除操作：删除后索引3处的元素 = " + array[3]);        // 预期输出：“删除操作：删除后索引3处的元素 = 0”        // 遍历操作        System.out.println("遍历操作：");        for (int i = 0; i < array.length; i++) {            System.out.println("索引" + i + "处的元素 = " + array[i]);        }        // 遍历的预期输出：        // "索引0处的元素 = 10"        // "索引1处的元素 = 20"        // "索引2处的元素 = 35"        // "索引3处的元素 = 0"        // "索引4处的元素 = 50"        // 搜索操作查找值为35的元素        System.out.println("搜索操作：搜索值35");        for (int i = 0; i < array.length; i++) {            if (array[i] == 35) {                System.out.println("值35在索引" + i + "处找到");                break;            }        }        // 预期输出：“值35在索引2处找到”        // 更新操作        array[1] = 25; // 更新第二个元素（索引1）        System.out.println("更新操作：更新后索引1处的元素 = " + array[1]);        // 预期输出：“更新操作：更新后索引1处的元素 = 25”        // 所有操作完成后的最终数组状态        System.out.println("最终的数组状态：");        for (int value : array) {            System.out.println(value);        }        // 最终状态的预期输出：        // "10"        // "25"        // "35"        // "0"        // "50"    }}

何时应该使用数组？

数组在需要有组织的数据存储的各种情况下非常有用。它们非常适合处理名称、数字或标识符等项目列表。

数组在电子表格和数据库系统等软件应用中广泛使用。它们可靠的数据结构使它们非常适合需要快速访问数据的情况。它们还常用于排序和搜索算法中。

在预先知道数据集的大小的应用程序中，数组尤其有用。数组是更复杂数据结构的基础，因此作为开发人员，你必须理解它们的工作原理非常重要。

数组的优点和限制

数组提供对元素的快速访问，这是由于它们的连续内存分配所导致的。它们的简单性和易用性使它们成为编程中的热门选择。数组还提供了可预测的内存使用模式，增强了效率。

但是数组具有固定的大小，这限制了它们的灵活性。固定的大小可能导致空间浪费或容量不足的问题。向数组插入和删除元素可能效率低下，因为它们经常需要移动元素。

尽管存在这些限制，数组是程序员工具包中的基本工具，平衡了简单性和功能性。

要点

数组是用于有序、连续数据存储的主要数据结构。它们在许多情况下具有无与伦比的存储和管理数据集合的能力。

数组在编程中是基础，构建更复杂的结构和算法的基础。了解数组对于任何从事软件开发或数据处理的人都是必要的。

掌握数组使程序员具备有效管理数据的关键工具。从本质上讲，数组是许多复杂编程解决方案的基石。

4. 单向链表数据结构

将单向链表视为一系列连接在一线的火车车厢，其中每个车厢都是一个独立的数据元素。

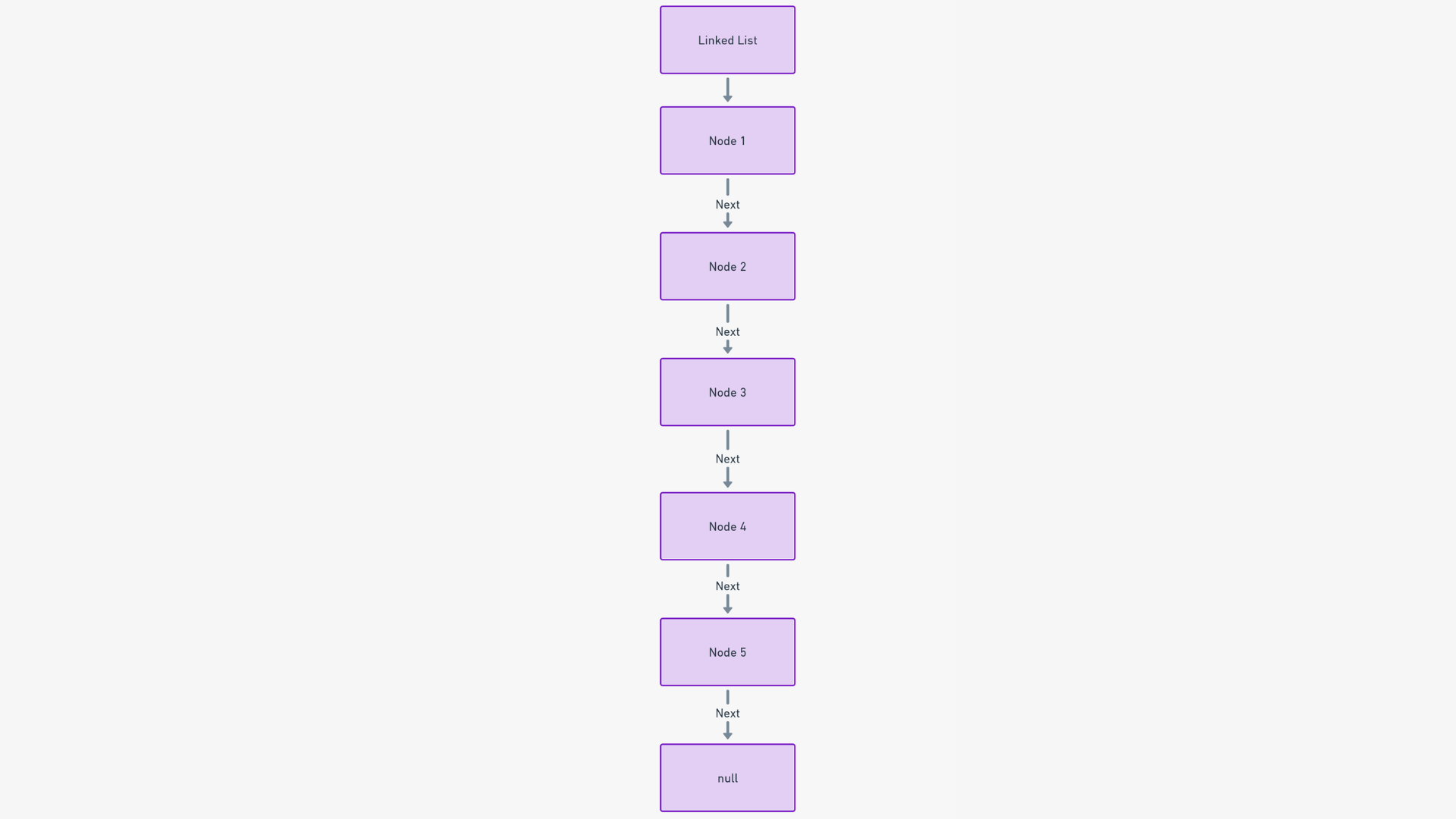
链表是一个连续的、动态的元素集合，被称为节点。每个节点指向它的后继节点，建立了一种链式的、可导航的结构。这种配置可以实现线性但适应性强的数据组织。

链表的作用是什么？

链表的核心功能是它们的顺序数据排列。每个节点既包含数据又包含对下一个节点的引用，将插入和删除等操作简化为高效的数据管理系统。

在数据结构的多样世界中，链表因其适应性而脱颖而出。它们在数据量动态变化的场景中尤其有价值，成为现代计算需求的灵活解决方案。

链表如何工作？

链表的结构是建立在节点上的。每个节点包括两个部分：数据本身和对下一个节点的指针。

想象一下宝藏寻找过程。每个线索（节点）不仅指引您找到一件宝藏（数据），还指引您找到下一个线索（下一个节点）。

链表的关键操作

链表的基本操作包括添加节点、删除节点、查找节点、遍历链表和更新链表。

• 添加节点：将新节点插入链表。
• 删除节点：高效地从链表中移除节点。
• 查找节点：通过遍历链表查找特定节点。
• 遍历链表：顺序移动遍历链表中的每个节点。
• 更新链表：允许修改现有节点中的数据。

什么时候使用链表？

链表在需要频繁插入或删除数据的环境中表现出色。它们的适用范围从为软件提供撤销功能到在操作系统中实现动态内存管理。

链表的优点和局限性

链表的主要优点在于它们的大小灵活性和插入和删除的效率。

但由于存储引用和依赖于顺序遍历，它们会增加内存使用量并且无法直接访问元素。

链表代码示例

让我们看一个使用链表管理动态任务列表的示例问题。

import java.util.LinkedList;public class LinkedListOperations {    public static void main(String[] args) {        LinkedList<String> list = new LinkedList<>();        // 添加操作        list.add("Node1");        System.out.println("添加 Node1 后: " + list); // 预期输出: [Node1]        list.add("Node2");        System.out.println("添加 Node2 后: " + list); // 预期输出: [Node1, Node2]        list.add("Node3");        System.out.println("添加 Node3 后: " + list); // 预期输出: [Node1, Node2, Node3]        // 删除操作        list.remove("Node2");        System.out.println("删除 Node2 后: " + list); // 预期输出: [Node1, Node3]        // 查找操作        boolean found = list.contains("Node3");        System.out.println("查找操作 - 节点3 在列表中吗？" + found); // 预期输出: true        // 遍历操作        System.out.print("遍历操作: ");        for(String node : list) {            System.out.print(node + " "); // 预期输出: Node1 Node3         }        System.out.println();        // 更新操作        list.set(0, "NewNode1");        System.out.println("将 Node1 更新为 NewNode1 后: " + list); // 预期输出: [NewNode1, Node3]        // 链表的最终状态        System.out.println("链表的最终状态: " + list); // 预期输出: [NewNode1, Node3]    }}

关键要点

链表是一种基本的动态数据结构，对于有效和灵活的数据管理至关重要。掌握链表对于所有开发人员来说都是至关重要的，它提供了简单性、灵活性和功能深度的独特结合。

5. 双向链表数据结构

双向链表是数据结构的一种演进。就像一条双向街道，每个节点都是一个有通向下一个和上一个节点的门的房子。

与它的单向链表表兄弟不同，这种结构使得节点可以同时知道它们的前任和继任者，这个特性从根本上改变了数据的遍历和操作方式。

双向链表作为一种更细腻、更多变的数据处理方式，反映了现实场景中的复杂性和相互关联性。

双向链表有什么作用？

双向链表是数据结构世界中的多面手，擅长前后数据导航。它们在需要数据灵活移动的应用程序中表现出色。

这种结构使用户能够轻松地前后跳转元素，这一特征在复杂数据序列中尤为重要，其中过去和未来的元素可能需要快速引用。

双向链表是如何工作的？

双向链表中的每个节点都是一个自包含的单元，由三个关键组成部分组成：它所包含的数据、指向下一个节点的指针和指向上一个节点的指针。

这个设置有点像一个播放列表，其中每首歌曲（节点）都知道它之前和之后的歌曲，允许在两个方向上进行流畅的切换。因此，该列表形成了一个双向的路径，通过其中的元素，使其比单向链表更加灵活。

双向链表的关键操作

双向链表的关键操作包括添加、删除、查找、迭代（正向和反向）和更新节点。

• 添加涉及在精确位置插入新元素。
• 删除是指从列表中取消链接并消除一个节点。
• 查找节点是更有效的，因为可以从任一端开始。
• 迭代特别灵活，允许在两个方向上进行遍历。
• 更新节点涉及修改现有数据，类似于修改日志中的条目。

何时使用双向链表？

双向链表在双向导航有益的系统中发挥作用。

它们用于浏览器历史记录中，允许用户在之前访问过的站点之间来回移动。在音乐播放器或文档查看器等应用程序中，它们使用户可以平滑、直观地在项目之间跳转。它们高效地插入和删除项目的能力也使它们适用于动态数据操作任务。

双向链表的优点和限制

双向链表在能够前后遍历方面表现出色，提供了单向链表无法匹敌的元素操作级别。这种独特的能力使得在复杂数据结构中通过前向和后向遍历数据成为可能，极大地增强了算法在复杂数据结构中的应用。但是，这种先进的功能要求进行妥协：每个节点需要两个指针（指向前一个和下一个节点），从而增加了内存消耗。

此外，与单向链表相比，双向链表的实现更加复杂。这可能会对初学者的代码维护和理解构成挑战。

尽管存在这些考虑因素，但双向链表仍然是动态数据场景中强大的选择，其中其灵活的结构优势超过了额外的内存和复杂性成本。

双向链表代码示例

class Node {    String data;    Node next;    Node prev;    Node(String data) {        this.data = data;    }}class DoubleLinkedList {    Node head;    Node tail;    // 向列表末尾添加节点的方法    void add(String data) {        Node newNode = new Node(data);        if (head == null) {            head = newNode;            tail = newNode;        } else {            tail.next = newNode;            newNode.prev = tail;            tail = newNode;        }    }    // 删除特定节点的方法    boolean remove(String data) {        Node current = head;        while (current != null) {            if (current.data.equals(data)) {                if (current.prev != null) {                    current.prev.next = current.next;                } else {                    head = current.next;                }                if (current.next != null) {                    current.next.prev = current.prev;                } else {                    tail = current.prev;                }                return true;            }            current = current.next;        }        return false;    }    // 查找节点的方法    boolean contains(String data) {        Node current = head;        while (current != null) {            if (current.data.equals(data)) {                return true;            }            current = current.next;        }        return false;    }    // 从头到尾打印列表的方法    void printForward() {        Node current = head;        while (current != null) {            System.out.print(current.data + " ");            current = current.next;        }        System.out.println();    }    // 从尾到头打印列表的方法    void printBackward() {        Node current = tail;        while (current != null) {            System.out.print(current.data + " ");            current = current.prev;        }        System.out.println();    }    // 更新节点数据的方法    boolean update(String oldData, String newData) {        Node current = head;        while (current != null) {            if (current.data.equals(oldData)) {                current.data = newData;                return true;            }            current = current.next;        }        return false;    }}public class DoubleLinkedListOperations {    public static void main(String[] args) {        DoubleLinkedList list = new DoubleLinkedList();        // 添加操作        list.add("节点1");        list.add("节点2");        list.add("节点3");        System.out.println("添加操作后:");        list.printForward(); // 预期输出: 节点1 节点2 节点3         // 删除操作        list.remove("节点2");        System.out.println("删除操作后:");        list.printForward(); // 预期输出：节点1 节点3        // 查找操作        boolean foundNode1 = list.contains("节点1");        boolean foundNode3 = list.contains("节点3");        System.out.println("查找操作 - 节点1在列表中吗？" + foundNode1); // 预期输出: true        System.out.println("查找操作 - 节点3在列表中吗？" + foundNode3); // 预期输出: true        // 正向遍历操作        System.out.print("正向遍历操作: ");        list.printForward(); // 预期输出: 节点1 节点3        // 反向遍历操作        System.out.print("反向遍历操作: ");        list.printBackward(); // 预期输出: 节点3
双向链表的实际应用
双向链表在需要频繁且高效地从列表两端插入和删除元素的应用中特别有用。
它们广泛应用于高级计算系统，如游戏应用程序，其中玩家的操作可能会导致游戏状态立即改变，或者在复杂软件中的导航系统中，允许用户遍历历史状态或设置。
另一个关键应用是在多媒体软件中，如照片或视频编辑工具，用户可能需要在编辑序列中前后移动。
它们的双向遍历能力还使它们成为实现缓存驱逐策略中使用的数据库管理系统中的高级算法的理想选择，其中元素的顺序需要频繁而高效地修改。
双向链表的性能方面
就性能而言，与其他数据结构相比，双向链表在某些方面提供了显着的优势，同时也有一些妥协。
在列表两端进行插入和删除操作的时间复杂度为O(1)，使得这些操作非常高效。但是在双向链表中搜索元素的时间复杂度为O(n)，因为可能需要遍历整个链表。与哈希表等数据结构相比，这种效率较低。
此外，为每个节点存储两个指针的额外内存开销是需要考虑的，特别是在内存敏感型应用中。这与数组和单向链表形成了对比，后者的内存使用通常较低。
然而，对于需要快速插入和删除的应用，并且数据集大小不是很大的情况下，双向链表提供了效率和灵活性的平衡。
关键要点
本质上，双向链表代表了数据管理的一种复杂方法，提供了增强的灵活性和效率。在进入更高级的数据结构实现时，您将希望了解它们。
双向链表在基本数据管理和更复杂数据处理需求之间起着桥梁的作用。这使它们成为程序员工具箱中用于复杂数据解决方案的重要组成部分。
6. 堆栈数据结构
想象一下堆栈就像是一个自助餐厅的盘子塔，唯一与盘子互动的方式就是从顶部添加或移除盘子。
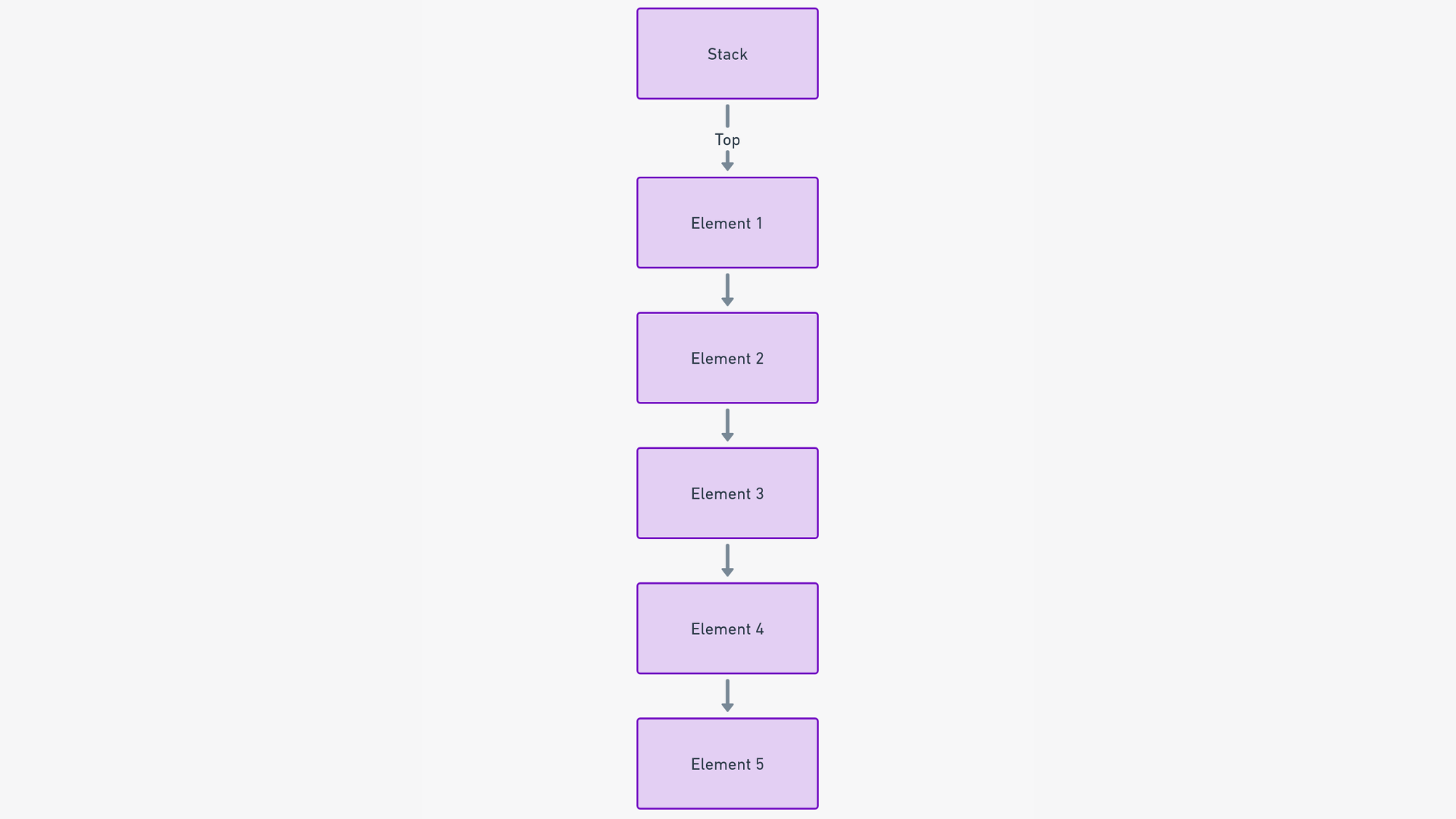
在数据结构的世界中，堆栈是一种线性有序元素的集合，严格遵循后进先出（LIFO）原则。这意味着最后添加的元素将首先被移除。尽管这听起来很简单，但对于数据管理来说，它的影响是深远而广泛的。
堆栈在计算机科学中作为基本概念，为许多复杂算法和功能提供基础。在本节中，我们将深入探讨堆栈，揭示它们在现代计算中的应用、操作和重要性。
堆栈的作用是什么？
堆栈的基本目的是以有序可逆的方式存储元素。其主要操作是从堆栈的顶部添加（推入）和移除（弹出）元素。这种看似简单的结构在需要立即访问最近添加数据的场景中具有巨大的重要性。
我们来考虑一些堆栈不可或缺的场景。在软件开发中，文本编辑器中的撤消机制依靠堆栈来存储变更历史。当您点击“撤消输入”时，实际上是从堆栈的顶部弹出元素，恢复到先前的状态。
类似地，通过浏览器的历史记录进行导航 - 点击“返回”或“前进” - 利用基于堆栈的结构来管理您访问过的页面。
堆栈如何工作？
为了理解堆栈的工作原理，让我们使用一个实际的类比：想象一摞书。在这个堆栈中，您只能与顶部的书籍互动。您可以在堆栈中添加一本新书，这本书成为新的顶部书籍，或者您可以移除顶部的书籍。这将导致形成符合LIFO原则的顺序。
如果您想要从堆栈的中间或底部访问一本书，您必须首先移除所有在它上面的书籍。 这个核心特点简化了不同应用程序中的数据管理，确保最近添加的项目始终是下一个要处理的项目。
关键堆栈操作
堆栈中的关键操作是其功能的基本组成部分。 让我们详细探讨每个操作：
Push 将元素添加到堆栈的顶部。 这就像在我们的自助餐厅类比中在堆栈顶部放置一个新盘子。
Pop 删除并返回堆栈的顶部元素。 这就像从堆栈中取出最上面的盘子。
Peek 允许您查看顶部的元素而不将其删除。 您可以将其视为没有实际拿掉顶部盘子的一瞥。
IsEmpty 检查堆栈是否为空。 验证我们的自助餐厅堆栈中是否还有任何盘子是至关重要的。
Search 帮助您找到堆栈中特定元素的位置。 它告诉您在堆栈中位于多远位置的一个项目。
这些操作是开发人员用来操作堆栈中的数据的工具，确保它保持有序和高效。
何时使用堆栈？
堆栈在各种场景中有应用。 一些常见用例包括：
撤消功能：在文本编辑器和其他软件中，使用堆栈来实现撤消和重做功能，允许用户恢复到之前的状态。
浏览器历史：当您在网络浏览器中向后或向前导航时，实际上是在遍历已访问页面的堆栈。
回溯算法：在人工智能和图遍历等领域，堆栈在回溯算法中发挥关键作用，实现对潜在路径的有效探索。
函数调用管理：当您在程序中调用一个函数时，调用堆栈中将添加一个堆栈帧，方便跟踪函数调用及其返回值。
这些示例强调了堆栈在现代计算中的普遍性，使其成为软件开发人员的基本概念。
堆栈的优势和限制
堆栈具有一系列的优点和限制。
优点：
简单性：堆栈的实现和使用都非常简单。
效率：它们提供了一种处理数据的高效方式，按照LIFO顺序。
可预测性：严格的LIFO顺序简化了数据管理，确保操作序列清晰。
限制：
有限访问：堆栈提供有限的访问权限，只能与顶部元素交互。 这限制了在需要访问更深层次堆栈元素的情况下的使用。
内存限制：如果推到极限，堆栈可能会耗尽内存，从而导致OutOfMemoryError。 在软件开发中，这是一个实际的问题。
尽管有其限制，由于其效率和可预测性，堆栈仍然是程序员工具箱中的关键工具。
堆栈代码示例
import java.util.Stack;public class AdvancedStackOperations {    public static void main(String[] args) {        // 创建一个堆栈来存储整数        Stack<Integer> stack = new Stack<>();        // 检查堆栈是否为空        boolean isEmpty = stack.isEmpty();        System.out.println("堆栈是否为空？" + isEmpty); // 输出：堆栈是否为空？true        // 将整数推入堆栈中        stack.push(10);        stack.push(20);        stack.push(30);        stack.push(40);        stack.push(50);        // 在推入整数后显示堆栈        System.out.println("推入整数后的堆栈：" + stack);        // 输出：推入整数后的堆栈：[10, 20, 30, 40, 50]        // 再次检查堆栈是否为空        isEmpty = stack.isEmpty();        System.out.println("堆栈是否为空？" + isEmpty); // 输出：堆栈是否为空？false        // 查看顶部整数而不删除它        int topElement = stack.peek();        System.out.println("查看顶部整数：" + topElement); // 输出：查看顶部整数：50        // 从堆栈中弹出顶部整数        int poppedElement = stack.pop();        System.out.println("弹出的整数：" + poppedElement); // 输出：弹出的整数：50        // 弹出整数后显示堆栈        System.out.println("弹出整数后的堆栈：" + stack);        // 输出：弹出整数后的堆栈：[10, 20, 30, 40]        // 在堆栈中搜索整数        int searchElement = 30;        int position = stack.search(searchElement);        if (position != -1) {            System.out.println("在堆栈中的 " + searchElement + " 的位置（从1开始计数）：" + position);        } else {            System.out.println(searchElement + " 未在堆栈中找到。");        }        // 输出：在堆栈中的 30 的位置（从1开始计数）：3    }}
栈的实际应用
栈数据结构在计算机科学和软件开发中具有广泛的实际应用。
它们常用于实现文本编辑器和设计软件中的撤消和重做功能，让用户可以高效地撤消或重做操作。
在网络浏览器中，栈使用户可以通过点击后退或前进按钮实现无缝导航浏览历史记录。
操作系统依赖栈来管理函数调用和执行上下文。人工智能、游戏和优化问题中的回溯算法也通过栈来跟踪选择和有效地回溯。
基于栈的架构还用于解析和计算数学表达式，实现复杂的计算。
栈的性能考虑
栈以其高效性而闻名，关键操作如push、pop、peek和isEmpty的时间复杂度都是O(1)，确保对顶部元素的快速访问。
但是栈有一些限制，其仅提供有限的对除顶部元素之外的元素的访问。这使得它们不太适合深层元素的检索。
在深度递归应用程序中，栈也会消耗大量的内存，因此需要谨慎地管理内存。尾递归优化和迭代方法是缓解栈内存问题的策略。
总而言之，栈数据结构为软件开发中的实际应用提供了高效的解决方案，但需要了解其限制并合理使用内存以实现最佳性能。
重点总结
栈是编程中一种重要的数据结构，提供了一种简单而有效的方式来管理数据，遵循后进先出（LIFO）原则。理解栈的工作原理和如何利用其关键操作对于开发人员来说非常重要，因为它们在各种计算机科学和编程场景中广泛应用。
无论您是在文本编辑器中实现撤消功能还是浏览网页浏览历史记录，栈是幕后英雄，使一切成为可能。掌握栈是成为熟练的软件开发人员的基本步骤。

7. 队列数据结构
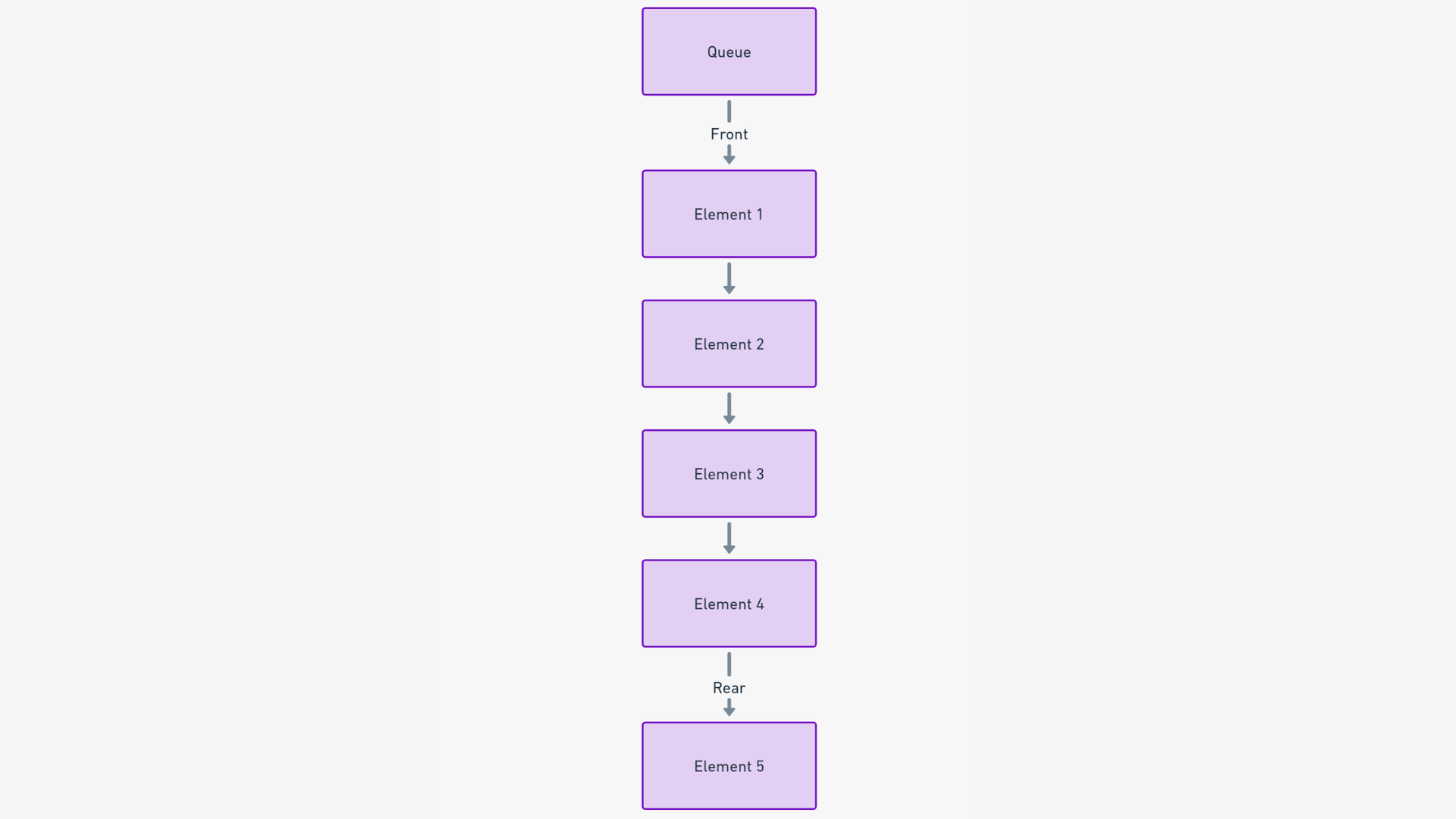
将队列视为 patiently 等待轮到他们的一排人的数字化等效物。就像现实生活中一样，队列数据结构遵循“先来先服务”（FIFO）原则。这意味着第一个添加到队列中的项目将首先被处理。
实质上，队列是一种线性数据结构，旨在以特定顺序保存元素，确保处理的顺序保持公平和可预测。
队列的作用是什么？
队列的主要功能是根据我们刚才讨论的FIFO原则来管理元素。它作为一个有序的集合，其中等待时间最长的元素最先获得机会。
现在，您可能会想知道为什么队列在计算机科学领域如此重要。答案在于它在确保任务按照特定顺序处理方面的重要性。
想象一下处理顺序很重要的情况，比如队列中的打印作业或键盘输入缓冲。队列确保这些任务以准确无误的方式执行，避免混乱并确保公平性。
队列是如何工作的？
为了理解队列的内部工作原理，让我们用一个现实生活的例子来解析它的基本机制。
在队列中，元素添加到队列的尾部，并从队列的头部移除。这个简单的操作确保等待时间最长的元素是下一个要处理的元素。
简单的示例：收银员售票场景
想象自己是一个售票员，正在售卖音乐会门票。您的队列由接近您的柜台的顾客组成。
根据FIFO原则，最先到达的顾客在队列的头部，最后到达的在尾部。当您按顺序为客户提供服务时，他们依次向队列前进，直到得到帮助然后离开。
关键队列操作
队列具有一组关键操作，使它们能够无缝地运行。

入队：将入队想象为顾客加入队伍。新元素被放置在队列末尾，耐心等待轮到它服务。
出队：出队类似于为队伍前面的顾客提供服务。队列头部的元素被移除，表示它已被处理完毕，现在可以离开队列。

虽然这些操作听起来很简单，但它们构成了队列功能的基础。
队列何时使用？
现在你已经了解了队列的工作原理，让我们来探讨一些使用场景：

键盘缓冲区：当你在键盘上快速输入时，计算机使用队列来确保字符按你按键的顺序显示在屏幕上。
打印机队列：在打印中，队列用于管理打印作业，确保它们按照初始化的顺序完成。

现实世界中的应用
想象一下在线服务中用户提交请求或任务的场景，例如从网站下载文件或在电子商务平台上处理订单。这些请求通常基于“先到先服务”的原则处理，就像数字队列一样。
同样，在多人在线游戏中，玩家通常会在进入游戏之前加入游戏服务器的队列，确保按照加入的顺序为他们提供服务。
在这些数字场景中，队列在高效管理和处理数据或请求方面起着关键作用。
队列示例代码
为了真正理解队列的威力，让我们深入一个实际例子。
假设你的任务是实现一个能够处理呼叫中心客户服务请求的系统。每个请求被分配了一个优先级，你需要确保高优先级请求在低优先级请求之前被处理。
为了解决这个问题，你可以使用队列的组合。为每个优先级创建单独的队列，并按照优先级顺序处理请求。下面是一个简化的Java代码片段来说明这个概念：
Queue<CustomerRequest> highPriorityQueue = new LinkedList<>();Queue<CustomerRequest> mediumPriorityQueue = new LinkedList<>();Queue<CustomerRequest> lowPriorityQueue = new LinkedList<>();// 根据优先级入队请求highPriorityQueue.offer(highPriorityRequest);mediumPriorityQueue.offer(mediumPriorityRequest);lowPriorityQueue.offer(lowPriorityRequest);// 按优先级顺序处理请求processRequests(highPriorityQueue);processRequests(mediumPriorityQueue);processRequests(lowPriorityQueue);
这段代码确保高优先级请求在中优先级和低优先级请求之前被处理，保持公平性同时解决不同紧急程度的问题。
让我们看一个在代码中使用队列的另一个示例：
import java.util.LinkedList;import java.util.Queue;public class QueueOperationsExample {    public static void main(String[] args) {        // 使用LinkedList创建一个队列        Queue<String> queue = new LinkedList<>();        // 入队：向队列中添加元素        queue.offer("Customer 1");        queue.offer("Customer 2");        queue.offer("Customer 3");        // 入队后显示队列        System.out.println("入队后的队列：" + queue);        // 预期输出：入队后的队列：[Customer 1, Customer 2, Customer 3]        // 出队：移除队列头部的元素        String servedCustomer = queue.poll();        // 显示已服务的顾客和更新后的队列        System.out.println("已服务的顾客：" + servedCustomer);        // 预期输出：已服务的顾客：Customer 1        System.out.println("出队后的队列：" + queue);        // 预期输出：出队后的队列：[Customer 2, Customer 3]        // 入队更多顾客        queue.offer("Customer 4");        queue.offer("Customer 5");        // 入队更多顾客后显示队列        System.out.println("入队更多顾客后的队列：" + queue);        // 预期输出：入队更多顾客后的队列：[Customer 2, Customer 3, Customer 4, Customer 5]        // 再次出队一个顾客        String servedCustomer2 = queue.poll();        // 显示已服务的顾客和更新后的队列        System.out.println("已服务的顾客：" + servedCustomer2);        // 预期输出：已服务的顾客：Customer 2        System.out.println("出队后的队列：" + queue);        // 预期输出：出队后的队列：[Customer 3, Customer 4, Customer 5]    }}
队列的优势和局限性
每种数据结构都有其自身的优点和缺点，队列也不例外。
队列的一个关键优势是能够维护顺序。它确保在处理元素时公平和可预测。当顺序很重要时，队列是首选的数据结构。
但队列也有局限性。它们无法根据除了到达时间以外的任何标准来设置元素优先级。如果您需要处理具有不同优先级的元素，可能需要用其他数据结构或算法来补充队列。
关键要点
队列数据结构基于“先进先出”（FIFO）原则，对于维护顺序至关重要。它涉及到在尾部添加（入队）和在头部移除（出队）。
现实世界的应用包括键盘缓冲区和打印机队列。

8. 树状数据结构
想象一棵树-不仅仅是任何一棵树，而是一种精心构造的层次结构，可以彻底改变您存储和访问数据的方式。这不仅仅是一个理论概念-它是计算机科学和各个行业广泛使用的强大工具。
树状数据结构的作用是什么？
树状数据结构的主要功能是按层次排列数据，创建一个模拟现实世界层次结构的结构。
这为什么重要？你可能会问。考虑一下：它是文件系统的支柱，确保高效的层次数据表示，并在优化搜索操作方面表现出色。如果要高效地管理具有层次结构的数据，树状数据结构是您的首选。
树状数据结构如何工作？
树的内部机制既简单又灵活。想象一棵家谱树，其中每个个体都是与其父母连接的节点。
树中的节点通过父子关系链接在一起，顶部有一个根节点。就像真实的家谱树一样，信息从根部传递到叶子，创建了一个结构化的层次结构。
无论是在计算机中组织文件还是表示公司的结构，树都为处理层次数据提供了明确而高效的方法。
关键的树操作
理解树的关键操作对于实际使用至关重要。这些操作包括添加节点、删除节点和遍历树。让我们深入了解每个操作的重要性：
添加节点
向树中添加节点类似于扩展其层次结构。此操作允许您无缝地合并新的数据点。
当您添加节点时，将现有节点（父节点）与新节点（子节点）建立连接。这种关系表示了数据的层次结构。
添加节点的实际场景包括将新文件插入文件系统或向组织图表中添加新员工。
删除节点
删除节点是维护树的完整性的关键操作。它可以使您修剪不必要的分支或数据点。
当您删除节点时，将断开其与树的连接，有效地消除它及其子结构。对于删除文件系统中的文件或处理组织层次结构中的员工离职，此操作非常重要。
遍历树
遍历树类似于在其分支中导航以访问特定的数据点。树的遍历对于高效检索信息至关重要。
有各种遍历技术，每种技术都有其自己的用例：

中序遍历按升序访问节点，在二叉搜索树中常用于按排序顺序检索数据。
前序遍历在处理其子节点之前处理当前节点，适用于复制树结构。
后序遍历在处理其子节点之后处理当前节点，适用于删除树或计算数学表达式。

树遍历操作提供了实际手段来探索和处理分层数据，使其在各种应用中易于访问和使用。
通过掌握这些关键操作，您可以有效地管理分层数据结构，使树成为计算机科学和软件工程中的宝贵工具。
无论您需要组织文件、表示家族关系还是优化数据检索，对这些操作的充分理解将赋予您对树结构的完全潜力的驾驭能力。
树的性能问题
现在，让我们深入实际的性能领域，这是树数据结构的一个关键方面。
性能完全关乎效率，也就是面对现实世界的数据时，您能够多快地执行树上的操作。
让我们通过检查常见树操作的时间和空间复杂度来分解它。
常见操作的时间和空间复杂度
插入：当您向树中添加新数据时，您能以多快的速度完成？插入的时间复杂度取决于树的类型。
例如，在平衡二叉搜索树（如AVL或红黑树）中，插入的时间复杂度为O(log n)，其中n是树中的节点数。
但是在不平衡的二叉树中，最坏情况下可能达到O(n)。插入的空间复杂度通常为O(1)，因为它只涉及添加一个单一节点。
删除：从树中删除数据应该是一个顺畅的过程。与插入类似，删除的时间复杂度取决于树的类型。
在平衡的二叉搜索树中，删除也具有O(log n)的时间复杂度。但是在不平衡树中，它可以是O(n)。删除的空间复杂度为O(1)。
遍历：遍历树，无论是为了搜索、检索数据，还是按特定顺序处理数据，都是一种基本操作。遍历方法的时间复杂度可能有所不同：

中序、前序和后序遍历的时间复杂度为O(n)，因为它们正好访问每个节点一次。
使用队列的层序遍历也具有O(n)的时间复杂度。遍历方法的空间复杂度通常取决于遍历过程中使用的数据结构。例如，使用队列的层序遍历的空间复杂度为O(w)，其中w是树的最大宽度（最宽级别的节点数）。

空间复杂度和内存使用
虽然时间复杂度涉及速度，但空间复杂度涉及内存使用。树可以影响应用程序消耗的内存量，在资源受限的环境中这非常重要。
整个树结构的空间复杂度取决于其类型和平衡性：

在平衡的二叉搜索树（如AVL、红黑树）中，空间复杂度为O(n)，其中n是节点数。
在B树中，它们用于数据库和文件系统，空间复杂度可以更高，但旨在高效存储大量数据。
在不平衡的树中，空间复杂度也可能是O(n)，使其内存利用效率较低。

通过深入研究时间和空间复杂度的实际方面，您将具备在项目中使用树结构时做出明智决策的能力。
无论是优化数据存储、加速搜索还是确保高效的数据管理，这些见解都将指导您有效地实施树结构。
树代码示例
import java.util.LinkedList;import java.util.Queue;// 表示树中单个节点的类class TreeNode {    int value; // 节点的值    TreeNode left; // 指向左子节点的指针    TreeNode right; // 指向右子节点的指针    // 构造函数用于创建具有给定值的新节点    public TreeNode(int value) {        this.value = value;        this.left = null; // 将左子节点初始化为null        this.right = null; //将右子节点初始化为null    }}// 表示二叉搜索树的类class BinarySearchTree {    TreeNode root; // BST的根节点    // 构造函数创建一个空的BST    public BinarySearchTree() {        this.root = null; //将根节点初始化为null    }    // 公共方法将一个值插入BST中    public void insert(int value) {        // 调用私有递归方法以插入值        root = insertRecursive(root, value);    }    // 私有递归方法从给定节点开始插入值    private TreeNode insertRecursive(TreeNode current, int value) {        if (current == null) {            // 如果当前节点为null，使用给定值创建一个新节点            return new TreeNode(value);        }        // 决定将值插入左子树还是右子树        if (value < current.value) {            // 在左子树中插入            current.left = insertRecursive(current.left, value);        } else if (value > current.value) {            // 在右子树中插入            current.right = insertRecursive(current.right, value);        }        // 返回当前节点        return current;    }    // 公共方法进行BST的中序遍历    public void inOrderTraversal() {        System.out.println("中序遍历:");        // 从根节点开始递归中序遍历        inOrderRecursive(root);        System.out.println();        // 期望输出: "20 30 40 50 60 70 80"    }    // 私有递归方法进行中序遍历    private void inOrderRecursive(TreeNode node) {        if (node != null) {            // 遍历左子树，访问节点，然后遍历右子树            inOrderRecursive(node.left);            System.out.print(node.value + " ");            inOrderRecursive(node.right);        }    }    // 公共方法进行BST的前序遍历    public void preOrderTraversal() {        System.out.println("前序遍历:");        // 从根节点开始递归前序遍历        preOrderRecursive(root);        System.out.println();        // 期望输出: "50 30 20 40 70 60 80"    }    // 私有递归方法进行前序遍历    private void preOrderRecursive(TreeNode node) {        if (node != null) {            // 访问节点，然后遍历左子树和右子树            System.out.print(node.value + " ");            preOrderRecursive(node.left);            preOrderRecursive(node.right);        }    }    // 公共方法进行BST的后序遍历    public void postOrderTraversal() {        System.out.println("后序遍历:");        // 从根节点开始递归后序遍历        postOrderRecursive(root);        System.out.println();        // 期望输出: "20 40 30 
树的优势和局限性
了解树的优点和缺点至关重要。树有各种优势，例如高效的分层数据检索。但在某些情况下，树可能不是最佳选择，例如非结构化数据。
在何时何地使用这种强大的数据结构需要做出明智的决策。
要点
树是实用工具，可以彻底改变您组织和访问层次数据的方式。
无论您是构建文件系统还是优化搜索算法，树数据结构都是您在数据结构领域中可信赖的伙伴。
9. 图数据结构
图数据结构在计算机科学中占据关键地位，类似于一个由互相连接的节点和边组成的网络。
在本质上，图表示一组通过边连接的节点（或顶点）- 每个节点可能包含一段数据，并且每条边表示一种关系或连接。
现在，我们将深入探讨图数据结构的本质、功能和现实世界的应用。
图数据结构的作用是什么？
图主要模拟各种实体之间的复杂关系和连接。它们具有社交网络、道路地图和数据网络等各种应用。
通过了解图，您可以把握我们数字和物质世界中许多复杂系统的基本结构。
图如何工作？
图通过节点之间的边连接而起作用。以非技术示例为例：一座城市的道路地图或一个社交网络。它们代表了连接（边）点（节点）的图，创造了一个网络。
图数据结构中的关键操作
在图数据结构中，您需要了解一些关键操作，用于构建、分析和修改网络。这些操作包括添加和删除节点和边，以及分析图中的连接和关系。
添加节点（顶点）涉及将一个新节点插入图中，这是构建图结构的初始步骤，对于扩展网络至关重要。
删除节点（顶点）涉及删除节点及其关联的边，从而改变图的配置。这是修改图的布局和连接的关键步骤。
添加边或建立两个节点之间的连接是图构建的基础。在无向图中，该连接是双向的，而在有向图中，边是从一个节点到另一个节点的单向链接。
删除边是改变图中关系和路径的关键步骤。
检查相邻性或确定两个节点之间是否存在直接的边，对于理解它们的相邻性、揭示图中的直接连接非常重要。
寻找邻居或识别直接连接到特定节点的所有节点对于探索和理解图的结构至关重要，因为它揭示了任何给定节点的直接连接。
图遍历使用深度优先搜索（DFS）和广度优先搜索（BFS）等系统方法，可以全面地探索图中的所有节点。
搜索操作包括定位特定节点或确定节点之间的路径，通常采用遍历技术来遍历图。
图操作的代码示例
import java.util.*;public class Graph {    // 用于存储图边的邻接列表    private Map<Integer, List<Integer>> adjList;    // 用于检查图是否是有向的布尔值    private boolean directed;    // 初始化图的构造函数，带有有向/无向标志    public Graph(boolean directed) {        this.directed = directed;        adjList = new HashMap<>();    }    // 添加新节点到图的方法    public void addNode(int node) {        // 如果节点不存在，则将节点放入邻接列表        adjList.putIfAbsent(node, new ArrayList<>());    }    // 从图中删除节点的方法    public void removeNode(int node) {        // 从其他节点的邻接列表中删除该节点        adjList.values().forEach(e -> e.remove(Integer.valueOf(node)));        // 从图中删除该节点        adjList.remove(node);    }    // 在两个节点之间添加边的方法    public void addEdge(int node1, int node2) {        // 将 node2 添加到 node1 的邻接列表        adjList.get(node1).add(node2);        // 如果图是无向的，则将 node1 添加到 node2 的邻接列表        if (!directed) {            adjList.get(node2).add(node1);        }    }    // 在两个节点之间删除边的方法    public void removeEdge(int node1, int node2) {        // 获取两个节点的邻接列表        List<Integer> eV1 = adjList.get(node1);       
图数据结构什么时候被使用？
图在建模社交网络、数据库关系和路由问题等场景中发挥作用。它们在各个行业和日常生活中的现实应用非常广泛，突显了它们在各个领域中的相关性。
了解何时以及如何使用图可大大提升您在许多领域中的问题解决能力。
图的优势和限制
图非常适合展示事物之间的联系，这非常有用。但有时候，它们并不是最好的选择，尤其是其他数据结构可能更快、更容易解决问题时。
当您决定是否使用图时，请考虑您想要做什么。如果事物之间存在复杂的相互关系，那么图可能是您需要的。但是，如果您的数据简单直接，可能更希望使用其他更易管理的数据结构。聪明选择，让您的工作闪耀起来。
实用代码示例
使用图数据结构有效解决的一个经典现实问题是在网络中找到最短路径。这在GPS系统的路线规划等应用中常见。该问题涉及在道路（或节点）网络中从起点到终点的最短路径。
为了阐明这一点，我们将使用迪杰斯特拉算法，这是一种用于在具有非负边权的图中找到最短路径的流行方法。以下是这个算法的Java实现以及一个简单的图设置，用于演示这个概念：
import java.util.*;public class Graph {    // 用于存储图的邻接列表的HashMap    private final Map<Integer, List<Node>> adjList = new HashMap<>();    // 表示图中节点的静态类    static class Node implements Comparable<Node> {        int node; // 节点标识符        int weight; // 到该节点的边的权重        // Node的构造函数        Node(int node, int weight) {            this.node = node;            this.weight = weight;        }        // 用于优先队列的compareTo方法重写        @Override        public int compareTo(Node other) {            return this.weight - other.weight;        }    }    // 添加节点到图的方法    public void addNode(int node) {        // 如果节点不存在，则将节点放入邻接列表中        adjList.putIfAbsent(node, new ArrayList<>());    }    // 添加边到图的方法    public void addEdge(int source, int destination, int weight) {        // 添加从源节点到目标节点的带有给定权重的边        adjList.get(source).add(new Node(destination, weight));        // 对于无向图，还要添加从目标节点到源节点的边        // adjList.get(destination).add(new Node(source, weight));    }    // 迪杰斯特拉算法，用于从起点到终点找到最短路径    public List<Integer> dijkstra(int start, int end) {        // 用于存储从起点到每个节点的最短距离的数组        int[] distances = new int[adjList.size()];        Arrays.fill(distances, Integer.MAX_VALUE); // 用最大值填充距离数组        distances[start] = 0; // 起点到自身的距离为0        // 用于探索节点的优先队列        PriorityQueue<Node> pq = new PriorityQueue<>();        pq.add(new Node(start, 0)); // 将起点节点添加到队列中        boolean[] visited = new boolean[adjList.size()]; // 用于跟踪已访问节点的访问数组        // 只要还有要探索的节点        while (!pq.isEmpty()) {            Node current = pq.poll(); // 获取具有最小距离的节点            visited[current.node] = true; // 将节点标记为已访问            // 探索当前节点的所有邻居节点            for (Node neighbor : adjList.get(current.node)) {                if (!visited[neighbor.node]) { // 如果邻居节点未被访问                    int newDist = distances[current.node] + neighbor.weight; // 计算新的距离                    if (newDist < distances[neighbor.node]) { // 如果新的距离较短                        distances[neighbor.node] = newDist; // 更新距离                        pq.add(new Node(neighbor.node, distances[neighbor.node])); // 将邻居节点添加到队列中                    }                }            }        }        // 从终点到起点重新构建最短路径        List<Integer> path = new ArrayList<>();        for (int at = end; at != start; at = distances[at]) {            path.add(at);        }        path.add(start);        Collections.reverse(path); // 将路径反转为起点到终点        return path; // 返回最短路径    }    // 主方法    public static void main(String[] args) {        Graph graph = new Graph(); // 创建一个新的图        // 添加节点和边到图中        graph.addNode(0);        graph.addNode(1);        graph.addNode(2);        graph.addNode(3);        graph.addEdge(0, 1, 1); // 从节点0到节点1的边，权重为1        graph.addEdge(1, 2, 3); // 从节点1到节点2的边，权重为3        graph.addEdge(2, 3, 1); // 从节点2到节点3的边，权重为1        graph.addEdge(0, 3, 10); // 从节点0到节点3的边，权重为10        // 执行迪杰斯特拉算法，找到最短路径        List<Integer> shortestPath = graph.dijkstra(0, 3); // 找到从节点0到节点3的最短路径        System.out.println("从节点0到节点3的最短路径：" + shortestPath); // 预期输出: [0, 1, 2, 3]    }}
在这段代码中，我们创建了一个带有四个节点（0、1、2、3）和它们之间带有指定权重的边的简单图。然后使用Dijkstra算法找到从节点0到节点3的最短路径。dijkstra方法计算从起始节点到所有其他节点的最短距离，然后我们重建最短路径到结束节点。
给定图的预期输出将是从节点0到节点3的最短路径，考虑边的权重。
关键要点
图数据结构在代表复杂网络和各个学科之间的关系方面至关重要。你现在理解了它们的关键作用和适应性，并了解了它们在解决现实世界问题中的实际应用和重要性。

10. 哈希表数据结构
在复杂的数据结构领域，哈希表以其高效性和实用性脱颖而出。哈希表是现代计算中的重要工具，对于希望优化数据检索和管理的任何人来说都是必不可少的。
哈希表是用来做什么的？
哈希表不仅仅是一个巧妙的概念 - 它们在数据管理中是一个强大的工具。它们在核心上存储键值对，实现了快速的数据检索。
为什么这是一个改变游戏规则的事情？哈希表对于简化数据库查询和关联数组是至关重要的。如果你的目标是快速访问数据和简化存储，哈希表将成为你工具箱中的一把利器。
哈希表如何工作？
哈希表在快速管理数据方面起着关键作用。《国际计算机科学与信息技术学术期刊》的一项研究指出，与传统方法相比，哈希表可以将数据检索速度提高多达50%。在数据量呈指数级增长的世界中，这种效率至关重要。
计算机科学家简·史密斯博士强调说：“在我们数据驱动的时代，理解和利用哈希表不是选择，而是提高效率所必需的。”
哈希表的关键操作
掌握哈希表的操作对于发挥它们的威力至关重要。这些操作包括：

添加元素：将新数据插入哈希表类似于将新书放在书架上。哈希函数处理键，将值精确定位到数组中的完美位置。这在缓存数据或存储用户配置文件等任务中至关重要。
删除元素：为了使哈希表像润滑的机器一样运行，删除元素是必不可少的。这个过程涉及擦除键值对，在刷新缓存条目或管理不断变化的数据集等场景中至关重要。
查找元素：在哈希表中查找元素就像在图书馆中找书一样简单。哈希函数使得检索与特定键关联的值成为一件轻而易举的事情，这是数据库查询和数据检索中的一个关键特性。
遍历元素：按元素顺序移动哈希表就像浏览书名列表一样。这个过程对于需要检查或处理所有存储数据的任务至关重要。

哈希表的性能考虑因素
性能是哈希表真正发挥优势的地方：

时间复杂度和空间复杂度：插入、删除和查找操作通常具有O(1)的时间复杂度，展示了哈希表的高效性。但在频繁碰撞的情况下，时间复杂度可能扩展到O(n)。遍历操作的时间复杂度为O(n)，取决于元素的数量。
空间复杂度和内存使用：哈希表通常具有O(n)的空间复杂度，反映了用于数据存储和数组结构的内存使用。

哈希表代码示例
import java.util.Hashtable;public class HashTableExample {    public static void main(String[] args) {        // 创建一个哈希表        Hashtable<Integer, String> hashTable = new Hashtable<>();        // 向哈希表添加元素        hashTable.put(1, "Alice");        hashTable.put(2, "Bob");        hashTable.put(3, "Charlie");        // 哈希表现在包含：{1=Alice, 2=Bob, 3=Charlie}        System.out.println("添加的元素：" + hashTable); // 输出：添加的元素：{3=Charlie, 2=Bob, 1=Alice}        // 从哈希表中删除元素        hashTable.remove(2);        // 删除后的哈希表：{1=Alice, 3=Charlie}        System.out.println("删除键2后：" + hashTable); // 输出：删除键2后：{3=Charlie, 1=Alice}        // 在哈希表中查找元素        String foundElement = hashTable.get(1);        // 找到键1对应的元素：Alice        System.out.println("找到键1对应的元素：" + foundElement); // 输出：找到键1对应的元素：Alice        // 遍历哈希表中的元素        System.out.println("遍历哈希表：");        for (Integer key : hashTable.keySet()) {            String value = hashTable.get(key);            System.out.println("键：" + key + "，值：" + value);            // 输出哈希表中每个元素        }    }}
哈希表的优点和局限性
哈希表提供快速的数据访问和高效的基于键的检索，使其在速度至关重要的场景下成为理想选择。
但在元素顺序至关重要的情况下，或者内存使用是主要考虑因素的情况下，它们可能不是最佳选择。
主要观点
哈希表不仅仅是一种数据结构 - 它们是数据管理中的战略工具。它们提高了数据检索和处理的效率，使其在现代计算中不可或缺。
随着我们在一个越来越数据中心的世界中航行，对哈希表的理解和应用已经不仅仅是有益的。对于那些希望在技术领域保持领先的人来说，这是必不可少的。

11. 如何释放数据结构在编程中的威力
数据结构是编程的基石，它将优秀的代码变成了卓越的代码。它们不仅仅是工具，而是塑造数据管理和利用方式的基础。
在编程中，掌握数据结构就像掌握了一种战略超能力，提升了软件的速度，效率和智能。当我们探索流行的数据结构时，请记住：这是让您的代码成为杰出之作的动力。
让代码效率提升：
数据结构的核心是用更少的资源实现更多功能。它们是您的代码性能加速器的关键。
想象一下：使用哈希表可以将缓慢的搜索操作变成闪电般的检索。或者考虑链表，它可以使添加或删除元素变得轻而易举。就像用高铁代替马车一样，为您的数据提供快速而高效的解决方案。
像专业人士一样解决问题：
数据结构是解决复杂问题的瑞士军刀。它们为您提供了一种分解和组织数据的方式，使得即使是最困难的问题也变得可以管理。
需要绘制层次结构？树会帮助您。处理网络数据？图是您的首选。关键是选择适合工作的正确工具。
灵活性在掌握：
数据结构的美在于它们的多样性。每种数据结构都带有自己特定的功能，可根据程序的需要进行部署。
这意味着您可以根据任务的需要调整方法，使您的软件更具适应性和健壮性。就像一个拥有完整香料架的厨师一样 - 可能性是无限的。
优化内存：
在编程世界中，内存就是黄金，数据结构帮助您明智地使用它。它们是内存的建筑师，高效地构建和管理内存。
例如，动态数组就像可扩展的存储单元，根据需要增长和收缩。通过掌握数据结构，您成为了内存的管理者，确保每个字节都不被浪费。
轻松应对扩展：
随着软件的增长，需求也随之增加。这是数据结构发挥作用的时候了。它们为扩展而构建。
例如，平衡的二叉搜索树在管理大型数据集方面表现优秀，无论大小如何，搜索和排序都快速。选择正确的数据结构意味着您的代码可以应对增长而不失效率。
主要观点
数据结构是支持杰出编程的支柱。它们为您的编码工具包带来效率、问题解决能力、适应性、内存优化和可扩展性。
理解并利用它们不仅仅是一种技能 - 在编程世界中，这是一种改变游戏规则的能力。拥抱这些强大工具，看着您的代码从优秀变为卓越。

12. 如何为您的应用程序选择正确的数据结构
选择正确的数据结构是软件开发中的关键决策，它直接影响您的应用程序的效率、性能和可伸缩性。
这不仅仅是选择一种工具 - 它是为了使您的代码与项目的需求相匹配，以实现最佳功能。让我们分解一下考虑这个关键选择的重要因素。
明确您的应用程序需求
第一步是了解您的应用程序的具体要求。您要处理什么类型的数据？您将执行哪些操作？是否有任何限制？
例如，如果快速搜索是一个优先考虑的问题，某些结构（如哈希表）可能是理想的选择。但如果您更关心高效的数据插入或删除，链表可能更适合。关键是将数据结构与您的独特需求匹配。
分析时间和空间复杂度
每种数据结构都具有自己的复杂性。二叉搜索树可能提供快速的搜索时间，但代价是更多的内存消耗。而简单数组可能在内存效率上更有优势，但搜索操作较慢。将这些因素与应用程序的性能目标进行权衡，以找到合适的平衡。
预测数据大小和增长
您的应用程序将处理多少数据，以及随着时间的推移，这可能会发生怎样的变化？对于小型或静态数据集，简单的数据结构可能足够。但如果您预计会有增长或需要处理大量数据，您将需要更强大的结构，比如平衡树或哈希表。
预测数据的变化轨迹是选择一个不仅在今天有效，而且在应用程序增长时仍能正常运行的结构的关键。
评估数据访问模式
您将如何访问数据？顺序访问还是随机访问？对这个问题的回答可以极大地影响您的选择。例如，数组在顺序访问方面表现出色，而哈希表在随机访问场景中表现出色。
了解您的访问模式有助于选择能够优化您最频繁操作的数据结构。
考虑内存限制
最后，考虑您的应用程序的内存环境。某些数据结构比其他结构更占用内存。如果您在有严格的内存限制的情况下工作，这可能是一个决定性因素。选择提供所需功能而不会过度负担系统内存的结构。
关键要点
总之，选择正确的数据结构意味着了解您应用程序的独特需求，并将其与不同结构的优势和限制相匹配。这是一个需要前瞻、分析和清晰把握项目目标的决策。
考虑这些因素后，您将具备充分的能力去做出可以提升应用程序性能和可伸缩性的选择。

13. 如何高效实现数据结构
在软件工程领域，选择和高效使用数据结构可以决定您系统的性能成败。下面是一个简明指南，确保您的数据结构不仅仅是实现，还能为最佳性能进行优化。
选择合适的工具
厨师根据要制作的食品选择刀具或搅拌机。同样，当您需要频繁在两端插入或删除元素时，使用链表会更合适，比如管理待办事项列表时，任务可能会改变优先级。
数组适用于游戏中静态的高分列表，而哈希表在开发联系人应用程序时，快速检索联系人详细信息至关重要。
了解选择的成本
考虑空间和时间的权衡。图形可能用于表示具有复杂连接的社交网络，但树对于组织公司的分层结构更有效，而堆栈可能是文本编辑器中撤销功能的最佳选择。
清晰和标准的代码
就像写菜谱一样，其他人可以轻松跟随。使用描述性的变量名，比如'maxHeight'而不是'mh'，并且对复杂算法的目的进行注释，这样可以使未来的更新或同事（或自己）调试变得更加顺利。
为意外做好准备
错误处理就像买保险一样，可能在不需要的时候看起来没必要，但在出现问题时非常重要。设置清晰的错误消息和后备机制，以防文件未找到或网络请求失败，就像GPS应用程序在原路径不可用时提供替代路线一样。
精心管理内存
就像在烹饪时保持厨房整洁一样。避免内存泄漏，释放C语言等语言中的内存，就像在做饭时随时清理一样，这样你就不会有一个杂乱的工作空间，更糟糕的是，程序不会因为使用了所有可用内存而崩溃。
测试，然后再测试一些
就像在发布文章之前多次校对一样。全面的测试应该包括边缘情况，比如你的堆栈数据结构在为空或已满时如何处理推入和弹出操作，确保在你的应用上线时能提供无缝的体验。
永不停止优化
持续改进你的代码，就像编辑者擦亮手稿一样。性能分析可能会揭示出将列表更改为集合的函数在检查成员资格时可以显著提高速度，就像使用更高效的路线减少旅行时间一样。跟上最新的算法，根据需要重构代码，保持领先。
重要经验教训
精通数据结构意味着做出明智选择，编写清晰且易于维护的代码，为意外情况做好准备，明智地管理资源，并致力于持续的测试和优化。正是这些实践将优秀的软件转变为出色的软件，确保你的数据结构不仅仅被实现，而且能够发挥其最佳性能。

14. 如何优化性能：了解数据结构的时间复杂性
在计算机科学的世界里，数据结构不仅仅是存储机制，它们是效率的构建者。了解如何操作和处理它们的时间复杂性不仅仅有用，它可以改变游戏规则，优化你的算法，提升软件性能。
让我们分解最常见的操作和它们的时间复杂性。
插入：（O(1)到O(n)）
插入就像向你的团队新增一名队员。在某些结构中，快速而简单，而在其他结构中则更耗时。
例如，在链表的开头添加一个元素是一个迅速的O(1)操作。但是，如果你在末尾插入，可能需要O(n)的时间，因为你可能需要遍历整个链表。
删除：（O(1)到O(n)）
把删除想象成是拿走一个拼图块。在某些情况下，比如从数组或链表中删除特定索引，这是一个迅速的O(1)操作。但在二叉搜索树或哈希表等结构中，你可能需要进行完整的O(n)遍历来找到并删除目标。
搜索：（O(1)到O(n)）
搜索就像在大海捞针一样。在数组或哈希表中，通常是一个闪电般快速的O(1)过程。但在二叉搜索树或链表中，你可能需要逐个遍历每个元素，将时间复杂性推向O(n)。
访问：（O(1)到O(n)）
访问数据就像从书架上拿书一样。在数组或链表中，通过特定索引获取元素是一个快速的O(1)任务。但是在更复杂的数据结构，如二叉树或哈希表中，你可能需要通过多个节点进行导航，导致O(n)的时间复杂度。
排序：(O(n log n) to O(n²))
排序是把你的鸭子排成一排的事情。效率根据你选择的算法而有很大的变化。
经典的快速排序、归并排序和堆排序通常在O(n log n)的范围内操作。但要小心那些效率较低的方法，其复杂度可能上升到O(n²)。
关键要点
当选择使用哪种数据结构时，理解这些时间复杂度非常重要。这与为工作选择合适的数据结构有关，确保你的软件不仅能工作，而且能高效工作。
无论是构建新应用程序还是优化现有应用程序，这些见解都是你实现高性能解决方案的路线图。

15. 数据结构在实际中的应用示例
数据结构不仅仅是理论概念；它们是我们日常使用的许多技术背后的无声强大力量。它们在组织、存储和管理数据方面起着至关重要的作用，使我们的数字体验变得无缝和高效。
让我们来探索这些技术世界的无名英雄如何在各种应用中产生真正的影响。
文本编辑器中的撤消功能：
在文本编辑器中按下“撤消”并惊叹于它如何恢复你的最后一次操作？这是堆栈数据结构的工作原理。你执行的每个操作都被“推入”到堆栈中。按下“撤消”按钮，堆栈就会“弹出”最近的操作，将你的文档恢复到之前的状态。简单而巧妙。
社交网络平台：
像Facebook和Twitter这样的平台不仅仅是连接人们，它们还负责管理庞大的数据网络。在这里，图形数据结构发挥着作用。它们绘制出用户之间复杂的连接和互动网络，使好友推荐和关系跟踪等功能不仅成为可能，而且非常高效。
GPS导航系统：
曾经想知道你的GPS是如何计算最快路线的吗？它使用图形和树来表示道路网络，通过遍历这些数据来找到最短路径。这不仅仅是为了让你从A点到B点，更重要的是以最高效的方式完成。
电子商务推荐引擎：
当在线商店完美地根据你的购物习惯提供建议时，要感谢哈希表和树等数据结构。它们分析你的购物习惯、偏好和历史记录，利用这些数据来个性化推荐，往往准确得令人难以置信。
文件系统组织：
你的计算机能够快速存储和检索文件，这得益于数据结构。树有助于组织目录，使文件导航变得轻松。同时，链表和位图等方法可以跟踪存储空间，确保高效的文件管理。
搜索引擎索引：
像Google这样的搜索引擎快速提供相关结果的速度完全归功于数据结构。倒排索引将关键词链接到包含这些关键词的网页，而树和哈希表则存储这些信息以进行快速检索。这不仅仅是搜索，而是以闪电般的速度在数字海量数据中寻找细微之处。

16. 学习数据结构的必备工具
导航数据结构的世界可能令人畏惧，但正确的资源和工具可以将这个旅程变成一个启发性的经历。
无论您是初学者，还是希望加深自己的专业知识，以下精选的资源都是您在掌握数据结构艺术上的盟友。

CodesCode：一个免费学习编程的开源社区。它提供交互式编程挑战和项目，以及相关的文章和视频，加强您对算法和数据结构的理解。太棒了！
"算法导论"，作者：Cormen、Leiserson、Rivest 和 Stein：这本具有里程碑意义的书籍是一个算法智慧的宝库，深入介绍了数据结构的原理和技术。
"数据结构与算法：带有示例的注释参考"，作者：Granville Barnett 和 Luca Del Tongo：这是一本实用的指南，通过清晰的解释和实际示例揭秘了数据结构，非常适合自学者。
Coursera：一站式领先在线课程平台，来自著名大学，提供结构化的学习路径和实际作业，巩固对数据结构和算法的理解。
VisuAlgo：通过动画可视化将数据结构栩栩如生，简化了复杂的概念，使其更易于理解。
数据结构可视化：这个平台提供交互式可视化表示，让您探索和理解常见数据结构的机制。
LeetCode：一个庞大的编程挑战代码库，包括特定于数据结构的问题，以在实际环境中提升和磨炼您的编程技能。
HackerRank：拥有大量挑战的平台，是应用和提升您的数据结构实现技能的绝佳场所。
Stack Overflow：利用庞大的程序员社区的集体智慧，是解决问题和从经验丰富的开发人员那里获得见解的宝贵资源。
Reddit：发现数据结构讨论繁荣的编程社区，提供学习小组机会和资源推荐。

这些资源不仅是学习辅助工具，更是通往对数据结构更深入理解和实际应用的门户。记住，最佳的学习方法是与您个人的风格和节奏相一致。利用这些工具将您的数据结构知识提升到一个新的高度。

17. 结论和实际行动步骤
掌握了全面的数据结构知识，您现在可以充分利用它们的潜力。以下是要点和实际步骤，指导您持续的学习之旅：
实践和实验
通过在不同的编程语言中实现各种数据结构来应用您的知识。这种实践方法可以巩固您的理解并增强解决问题的能力。
探索高级结构：
深入了解树、图和散列表等更复杂的数据结构，超越基础知识。理解它们的细微差别将显著提升您解决复杂编程挑战的能力。
深入研究算法：
将数据结构知识与算法学习结合起来。熟悉排序、搜索和图遍历技术，以优化您的代码并高效解决复杂的计算问题。
保持了解和参与：
跟上不断发展的软件工程领域。关注行业博客、参加技术会议并参与编程社区，紧跟时代潮流。
合作和分享：
与开发社区中的同行合作。一起参与编码项目可以带来新的视角，并提高您的技能。参与开源项目也是回馈和巩固您的专业知识的绝佳方式。
展示您的技能：
建立一个展示您使用数据结构解决实际问题能力的作品集。这个实际展示您技能的作品集对于给潜在雇主或客户留下深刻印象非常有价值。
拥抱掌握数据结构的旅程。这是一条通往优化编码、高效解决问题、在软件工程界脱颖而出的道路。不断学习、实验和分享你的知识，观察职业生涯中新机会和进步的大门为你打开。

18. 总结
总之，学习如何使用数据结构是任何有抱负的软件工程师的基石。通过理解这些结构，您可以提高代码的性能，确保可扩展性，并构建强大的应用程序。
从基本的数组和链表到复杂的树和图，每个结构都提供了独特的优势和应用。
通过深入研究算法及其在实践中的应用来继续探索。保持好奇心，勤奋实践，并加入我们致力于软件工程卓越的专业人士社群。我们提供丰富的资源、课程和网络机会，支持您在这个充满活力的领域中的成长和成功。
资源
如果您渴望掌握数据结构，请查看LunarTech.AI的数据结构掌握训练营。这是一个完美的课程，适合那些对人工智能和机器学习感兴趣的人，重点关注在编码中有效使用数据结构。这个综合计划涵盖了基本的数据结构、算法和Python编程，并包括导师指导和职业支持。
此外，如果您想在数据结构方面更多练习，可以在我们的网站上探索以下资源：

Java数据结构掌握- 轻松应对编程面试：一本免费电子书，提升您的Java技能，重点关注数据结构以增强面试和专业技能。
基础Java数据结构- 激发你的编码能力：另一本免费电子书，深入研究Java基础知识、面向对象编程和人工智能应用。

访问我们的网站获取这些资源和更多关于训练营的信息。
与我联系：

关注我的LinkedIn，获取大量有关计算机科学、机器学习和人工智能的免费资源
访问我的个人网站
订阅我的数据科学和人工智能通讯

关于作者
我是Vahe Aslanyan，在计算机科学、数据科学和人工智能的交汇处。访问vaheaslanyan.com查看一个精确和进步的作品集。我的经验桥接了全栈开发和AI产品优化之间的差距，致力于以新的方式解决问题。
Vahe Aslanyan - 打造代码，塑造未来  进入Vahe Aslanyan的数字世界，每一次努力都带来新的见解，每一个障碍都为成长铺平道路。打造代码，塑造未来
通过推出一所顶级数据科学训练营和与行业顶尖专家合作的记录，我始终专注于将技术教育提升到普遍标准。
当我们完成《数据结构书》时，我衷心感谢您的时间。将多年的专业和学术知识凝结为这本手册的旅程是一次充实的努力。谢谢您与我共同追求，我热切期待见证您在技术领域的成长。

							
Computer Science
Data Structures
handbook