机器学习基础手册 – 关键概念,算法和Python代码示例
「机器学习基础手册 - 关键概念、算法和Python代码示例」
如果你计划成为机器学习工程师、数据科学家,或者想在面试前复习一下,那么这本手册适合你。
在这本手册中,我们将介绍作为数据科学家、机器学习工程师、机器学习研究员和AI工程师需要了解的关键机器学习算法。
在整个手册中,我将为每个机器学习算法提供带有Python代码的示例,以帮助您理解您所学的内容。
无论您是初学者还是对机器学习或AI有一些经验,本指南旨在帮助您以高水平理解机器学习算法的基础知识。
作为一名经验丰富的机器学习从业者,我很高兴与您分享我的知识和见解。
你将学到什么
- 2.1 线性回归和普通最小二乘法(OLS)
- 2.2 逻辑回归和MLE
- 2.3 线性判别分析(LDA)
- 2.4 逻辑回归 vs LDA
- 2.5 朴素贝叶斯
- 2.6 朴素贝叶斯 vs 逻辑回归
- 2.7 决策树
- 2.8 Bagging
- 2.9 随机森林
- 2.10 提升或集成技术(AdaBoost, GBM, XGBoost)
- 3.1 子集选择
- 3.2 正则化(Ridge和Lasso)
- 3.3 维度约简(PCA)
- 4.1 交叉验证:(验证集、LOOCV、K-Fold CV)
- 4.2 K-Fold CV中的最佳k
- 4.5 自助法
- 5.1 优化技术:批量梯度下降(GD)
- 5.2 优化技术:随机梯度下降(SGD)
- 5.3 优化技术:带动量的SGD
- 5.4 优化技术:Adam优化器
- 6.1 主要要点和下一步
- 6.2 关于作者 – 就是我!
- 6.3 如何进一步深入研究?
- 6.4 联系我

先决条件
为了充分利用本手册,如果您熟悉一些核心机器学习概念将会有帮助:
基本术语:
- 训练数据和测试数据:用于训练和评估模型的数据集。
- 特征:用于预测的变量,也称为独立变量。
- 目标变量:预测的结果,也称为因变量或响应变量。
机器学习中的过拟合问题
了解过拟合问题,以及它与偏差-方差权衡的关系以及如何解决它非常重要。本指南中我们将详细介绍正则化技术。详细了解请参考:
 Tatev Karen AslanyanTowards Data Science
Tatev Karen AslanyanTowards Data Science
初学者的基础阅读
如果你没有统计学知识,并希望学习或恢复对基本统计概念的理解,我推荐阅读这篇文章:数据科学基本统计概念
如果你想要了解关于启动数据科学和人工智能职业的全面指南,并获得关于如何找到数据科学工作的见解,你可以深入阅读我的之前的手册:启动你的数据科学与人工智能职业
在机器学习中使用的工具/语言
作为机器学习研究员或机器学习工程师,你可能会在日常工作中使用许多技术工具和编程语言。但在这篇手册中,我们将使用以下编程语言和工具:
- Python基础知识:变量、数据类型、结构和控制机制。
- 必备库:
numpy、pandas、matplotlib、scikit-learn、xgboost - 环境:熟悉Jupyter Notebooks或PyCharm作为集成开发环境。
以坚实的基础踏上机器学习之旅,将使你获得更为深刻和启发性的体验。
现在,我们开始吧!
第一章:什么是机器学习?
机器学习(ML)是人工智能(AI)的一个分支,指的是计算机能够从数据模式中自主学习并进行决策,而无需进行明确的编程。机器利用统计算法来提升系统的决策和任务性能。
在其核心,ML是一种通过从数据中学习来改进任务的方法。可以将其类比为通过提供示例来教导计算机做出决策,就像向孩子展示图片以教他们识别动物一样。
例如,通过分析购买模式,ML算法可以帮助在线购物平台推荐产品(就像亚马逊建议你可能喜欢的商品一样)。
或者想想通过识别不需要的邮件中的模式来标记垃圾邮件的电子邮件平台。利用ML技术,计算机悄悄地提升了我们日常的数字体验,使推荐更准确,保护我们的收件箱。
在这段旅程中,你将揭开机器学习的迷人世界,这是一个技术通过遇到的信息进行学习和成长。但在此之前,让我们先了解一些机器学习的基础知识,以便理解任何类型的机器学习模型。
机器学习的学习类型:
模型学习有三种主要方式:
- 有监督学习:模型根据标记数据进行预测(你拥有特征和标签,X和Y)
- 无监督学习:模型自主识别模式,没有标记数据(只有特征,没有响应变量,只有X)
- 强化学习:算法通过行动反馈进行学习。
模型评估指标:
在机器学习中,每当你训练一个模型时,你总是需要评估它。你将根据问题性质使用最常见的评估指标。
以下是每种模型类型最常见的机器学习模型评估指标:
1. 回归指标:
- MAE、MSE、RMSE:衡量预测值与实际值之间的差异。
- R-Squared:表示模型解释的方差。
2. 分类指标:
- 准确率:正确预测的百分比。
- 精确率、召回率、F1-Score:评估预测质量。
- ROC曲线、AUC:衡量模型的辨别能力。
- 混淆矩阵:比较实际与预测分类。
3. 聚类指标:
- 轮廓系数:评估聚类内对象的相似性。
- 戴维森堡丁指数:评估群集分离度。

第二章:最受欢迎的机器学习算法
在本章中,我们将简化基本的机器学习(ML)算法的复杂性。这将是一个对从数据科学家和机器学习工程师到AI研究人员的各种角色都有价值的资源。
我们将从2.1的线性回归和普通最小二乘法(OLS)开始,然后进入2.2探索逻辑回归和最大似然估计(MLE)。
第2.3节探讨了线性判别分析(LDA),与逻辑回归在2.4中进行对比。我们在2.5中介绍了朴素贝叶斯,同时与逻辑回归进行比较分析在2.6。
在2.7中,我们学习决策树,然后探索集成方法:2.8中的装袋法,2.9中的随机森林。接下来,我们讨论各种流行的提升技术,包括2.10中的AdaBoost,2.11中的梯度提升模型(GBM),并在2.12中以极限梯度提升(XGBoost)作为结尾。
我们在这里讨论的所有算法都是领域中基础且流行的,每个数据科学家、机器学习工程师和人工智能研究人员至少应了解到这个高级别。
请注意,我们在这里不会深入探讨无监督学习技术,也不会详细介绍每个算法。
2.1 线性回归
当两个变量之间的关系是线性的时候,你可以使用线性回归统计方法。它可以帮助你建模一个变量的单位变化,独立变量对另一个变量,即因变量的值的影响。
因变量通常被称为响应变量或解释变量,而独立变量通常被称为回归变量或解释变量。
当线性回归模型基于单个独立变量时,模型称为简单线性回归。但是当模型基于多个独立变量时,它被称为多元线性回归。
简单线性回归可以用以下表达式描述:
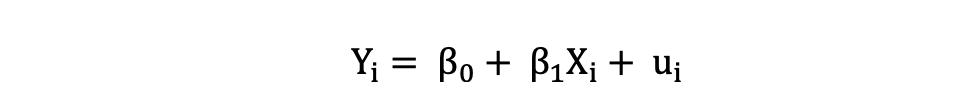
其中Y是因变量,X是数据中的独立变量,β0 是截距,未知且恒定,β1是斜率系数或与独立变量X对应的参数,也是未知且恒定的。最后,u是模型在估计Y值时产生的误差项。
线性回归背后的主要思想是通过一组配对的(X,Y)数据找到最佳拟合直线,即回归线。线性回归应用的一个例子是对企鹅身体质量的影响建模,其可视化如下:
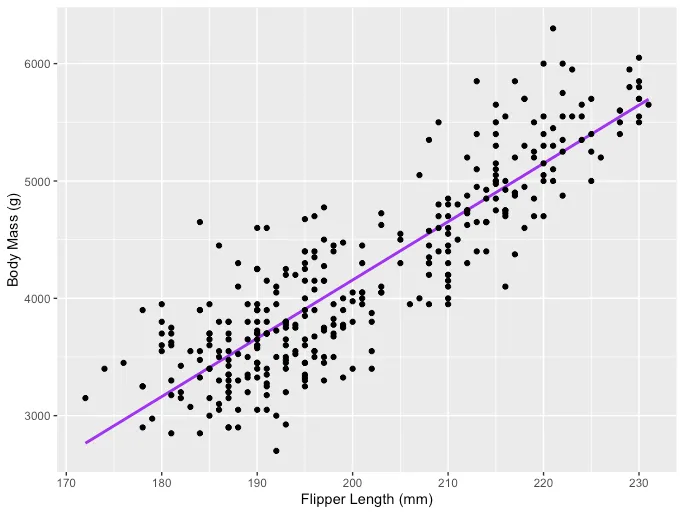
具有三个独立变量的多元线性回归可以通过以下表达式描述:
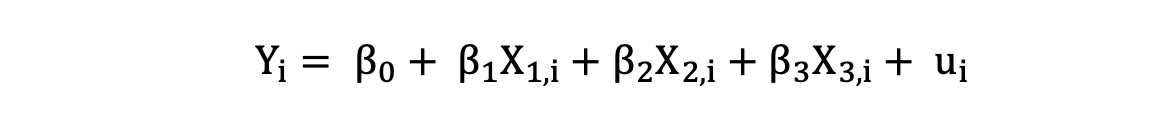
其中Y是因变量,X是数据中的独立变量,β0 是截距,未知且恒定,β1, β2, β3是斜率系数或与变量X1, X2, X3对应的参数,也是未知且恒定的。最后,u是模型在估计Y值时产生的误差项。
2.1.1 普通最小二乘法
普通最小二乘法(OLS)是一种估计线性回归模型中未知参数(如β0和β1 )的方法。该模型基于最小二乘法的原理,即最小化观察到的因变量与由独立变量的线性函数预测的值之间的差的平方和,通常称为拟合值。
实际值和预测值之间的差异被称为残差。OLS通过最小化残差的平方和来解决优化问题。此优化问题得出了未知参数β0和β1的OLS估计,这些估计也被称为系数估计。
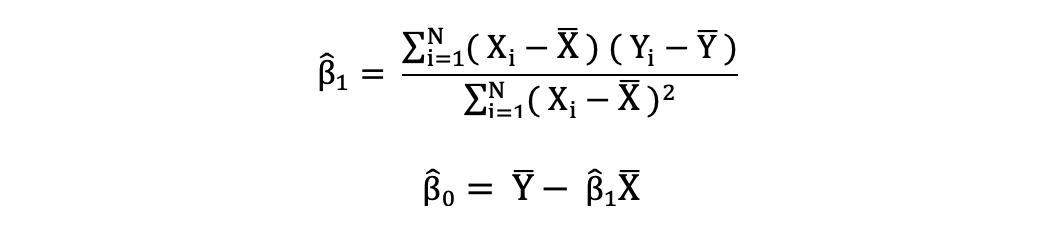
一旦估计了简单线性回归模型的这些参数,就可以计算响应变量的拟合值,如下所示:
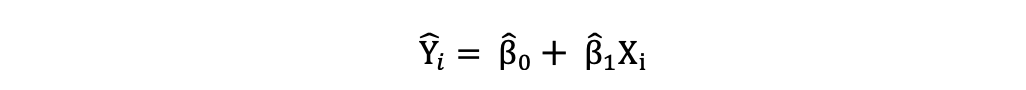
标准误差
可以按以下方式确定残差或估计的误差项:
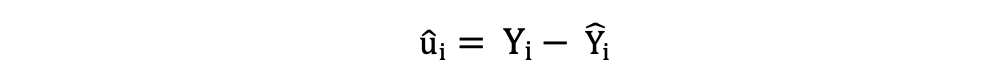
需要记住误差项和残差之间的区别。从未观测到误差项,而残差是从数据计算出来的。OLS为每个观测值估计了误差项,但没有估计实际误差项。因此,真正的误差方差仍然未知。
此外,这些估计值受到抽样不确定性的影响。这意味着在实证应用中,我们将永远无法从样本数据中确定这些参数的精确估计值。但是,我们可以通过计算样本残差方差来估计它。
2.1.2 OLS假设
OLS估计方法做出以下假设,为了获得可靠的预测结果,这些假设必须满足:
- 假设(A)1:线性假设表明模型在参数上是线性的。
- 假设2:随机样本假设表明样本中的所有观测值都是随机选择的。
- 假设3:外生性假设表明自变量与误差项不相关。
- 假设4:同方差性假设表明所有误差项的方差是恒定的。
- 假设5:没有完全多重共线性假设表明没有一个自变量是恒定的,并且自变量之间不存在精确的线性关系。
请注意,上述线性回归的描述来自我名为《线性回归完全指南》的文章。
有关线性回归的详细文章,请查看本篇文章:
 Tatev Karen AslanyanTowards AI
Tatev Karen AslanyanTowards AI
2.1.3 Python中的线性回归
假设你有一个朋友Alex,他收集邮票。每个月,Alex购买一定数量的邮票,你注意到他花费的金额似乎取决于购买的邮票数量。
现在,您想创建一个小工具,根据购买的邮票数量来预测Alex下个月将花费多少钱。这就是线性回归派上用场的地方。
从技术角度来说,我们正在试图根据独立变量(购买的邮票数量)来预测依赖变量(花费的金额)。
以下是使用scikit-learn执行线性回归的一些简单Python代码,针对创建的数据集进行线性回归。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import LinearRegression# 样本数据stamps_bought = np.array([1, 3, 5, 7, 9]).reshape((-1, 1)) # 重塑为2D数组amount_spent = np.array([2, 6, 8, 12, 18])# 创建线性回归模型model = LinearRegression()# 训练模型model.fit(stamps_bought, amount_spent)# 预测next_month_stamps = 10predicted_spend = model.predict([[next_month_stamps]])# 绘图plt.scatter(stamps_bought, amount_spent, color='blue')plt.plot(stamps_bought, model.predict(stamps_bought), color='red')plt.title('购买邮票 vs 花费金额')plt.xlabel('购买邮票数量')plt.ylabel('花费金额($)')plt.grid(True)plt.show()# 显示预测print(f"如果Alex下个月购买{next_month_stamps}张邮票,他们可能会花费${predicted_spend[0]:.2f}。")- 样本数据:
stamps_bought代表Alex每个月购买的邮票数量,amount_spent代表相应的花费金额。 - 创建和训练模型:使用
scikit-learn中的LinearRegression()创建和训练我们的模型,使用.fit()方法。 - 预测:使用训练好的模型来预测给定邮票数量下Alex将花费的金额。在代码中,我们预测了10张邮票的花费金额。
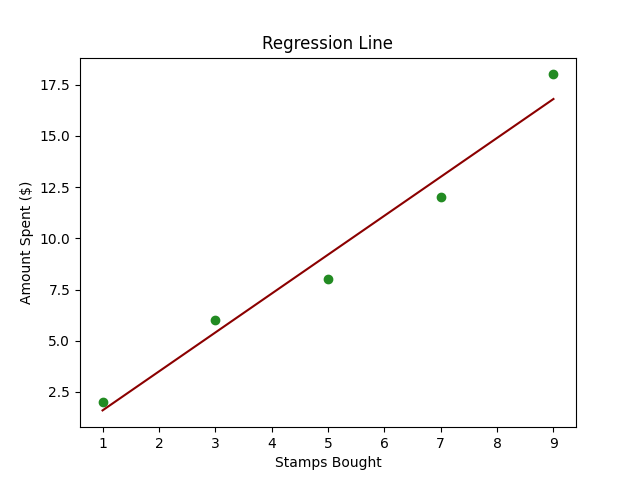
- 绘图:我们绘制原始数据点(蓝色)和预测线(红色),以直观地了解我们模型的预测能力。
- 显示预测:最后,我们打印出特定邮票数量(此处为10张)的预测花费。

2.2 逻辑回归
另一个非常流行的机器学习技术是逻辑回归,虽然它被称为回归,但实际上是一种有监督的分类技术。
逻辑回归是一种机器学习方法,它基于给定的独立变量数据集,对事件发生的条件概率或观测属于某个类别的概率进行建模。
当两个变量之间的关系为线性关系且因变量为分类变量时,您可能希望预测一个以概率形式(介于0和1之间的数字)表示的变量。在这些情况下,逻辑回归非常有用。
这是因为在逻辑回归的预测过程中,分类器预测每个观测属于某个类别的概率(一个介于0和1之间的值),通常是依赖变量的两个类别之一。
例如,如果您想预测在选举过程中,候选人根据候选人的声望分数、过去的成功和其他描述候选人的变量来确定候选人是否会当选的概率或可能性,您可以使用逻辑回归来建模这种概率。
因此,逻辑回归模型的预测对象不是响应变量,而是Y属于特定类别的概率。
它与线性回归相似,但不同之处在于它预测对数几率而不是Y。在统计术语中,我们对响应变量Y的条件分布进行建模,给定预测变量X。因此,逻辑回归有助于预测Y属于某个类别(0和1)的概率,给定特征X的条件概率P(Y|X=x)。
逻辑回归中的“逻辑(Logistic)”一词源自于该方法所基于的函数,即逻辑函数。逻辑函数确保对于过大或过小的值,相应的概率仍在【0,1之间】。
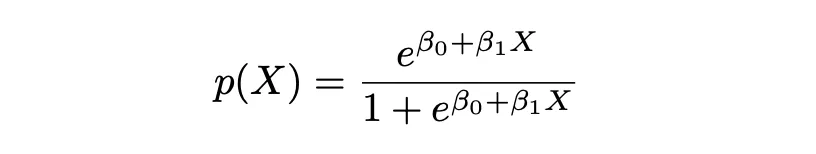
在以上方程中,P(X)代表给定特征P(Y|X=x)的类别Y(0和1)的概率。X代表自变量,β0 是截距,是未知的常数,β1是斜率系数或与未知的常数X变量相对应的参数,与线性回归类似。e 代表exp()函数。
概率比和对数几率
逻辑回归及其估计技术MLE是基于概率比和对数几率的术语。概率比定义如下:
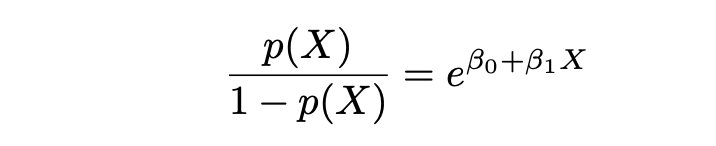
而对数几率定义如下:
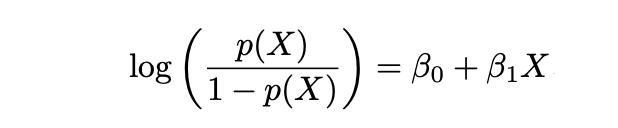
2.2.1 最大似然估计(MLE)
对于线性回归,我们使用OLS(最小二乘法)或LS(最小二乘法)作为估计技术,而对于逻辑回归,我们应使用另一种估计技术。
在逻辑回归中,我们不能使用LS找到最佳拟合线(进行估计),因为误差可能变得非常大或非常小(甚至为负),而在逻辑回归的情况下,我们的目标是预测值在[0,1]之间。
因此,对于逻辑回归,我们使用MLE技术,其中似然函数计算基于输入数据和模型观测到结果的概率。将优化此函数以找到产生训练数据集上最大概似总和的参数集。
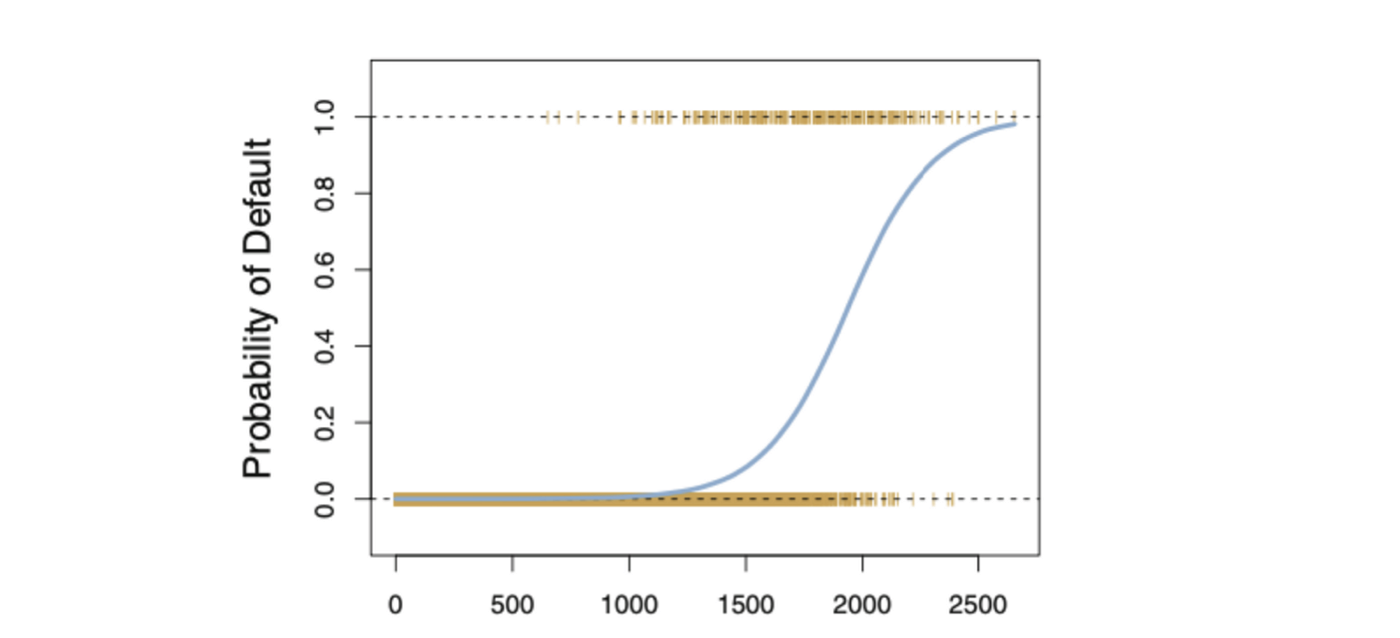
无论自变量X的值如何,逻辑函数始终会产生类似上图的S形曲线,从而大多数时候会得出合理的估计结果。
2.2.2 逻辑回归似然函数
似然函数可表示如下:
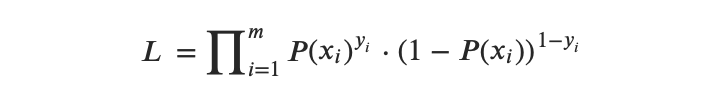
因此,对数似然函数可表示如下:
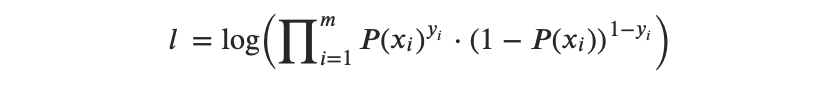
或者,从乘法转换为求和后,我们得到:
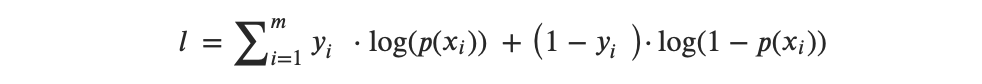
MSE的思想是找到一组估计,使得该似然函数最大化。
- 步骤1:将数据点投影到一个候选线上,产生样本的对数几率值。
- 步骤2:通过使用以下公式将样本的对数几率转换为样本概率:
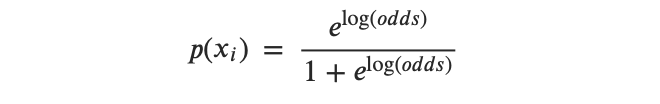
- 步骤3:获取总体概率或总体对数概率。
- 步骤4:一遍又一遍地旋转对数(赔率)线,直到找到最大化总体概率的最优对数(赔率)
2.2.3 逻辑回归中的截断值
如果您计划在最后使用逻辑回归获得二进制{0,1}值,则需要一个截断点将每个观测的估计值从[0,1]范围转换为值0或1。
根据您的个别情况,您可以选择相应的截断点,但常用的截断点是0.5。在这种情况下,所有预测值小于0.5的观测将被分配到类别0,而预测值大于或等于0.5的观测将被分配到类别1。
2.2.4 逻辑回归的性能度量
由于逻辑回归是一种分类方法,因此可以使用常见的分类度量标准,如召回率、精确率、F1度量。但也有一种度量系统也常用于评估逻辑回归模型的性能,称为偏差。
2.2.5 Python中的逻辑回归
Jenny是个热爱阅读的人。Jenny读各种类型的书,并在一个小日记中记录下书的页数以及她是喜欢还是不喜欢这本书。
我们发现一个模式:Jenny通常喜欢既不太短也不太长的书。现在,我们是否可以根据书的页数来预测Jenny是否会喜欢这本书呢?这就是逻辑回归可以帮助我们的地方!
从技术角度来说,我们试图根据一个独立变量(页数)来预测二元结果(喜欢/不喜欢)。
下面是一个使用scikit-learn来实现逻辑回归的简化Python示例:
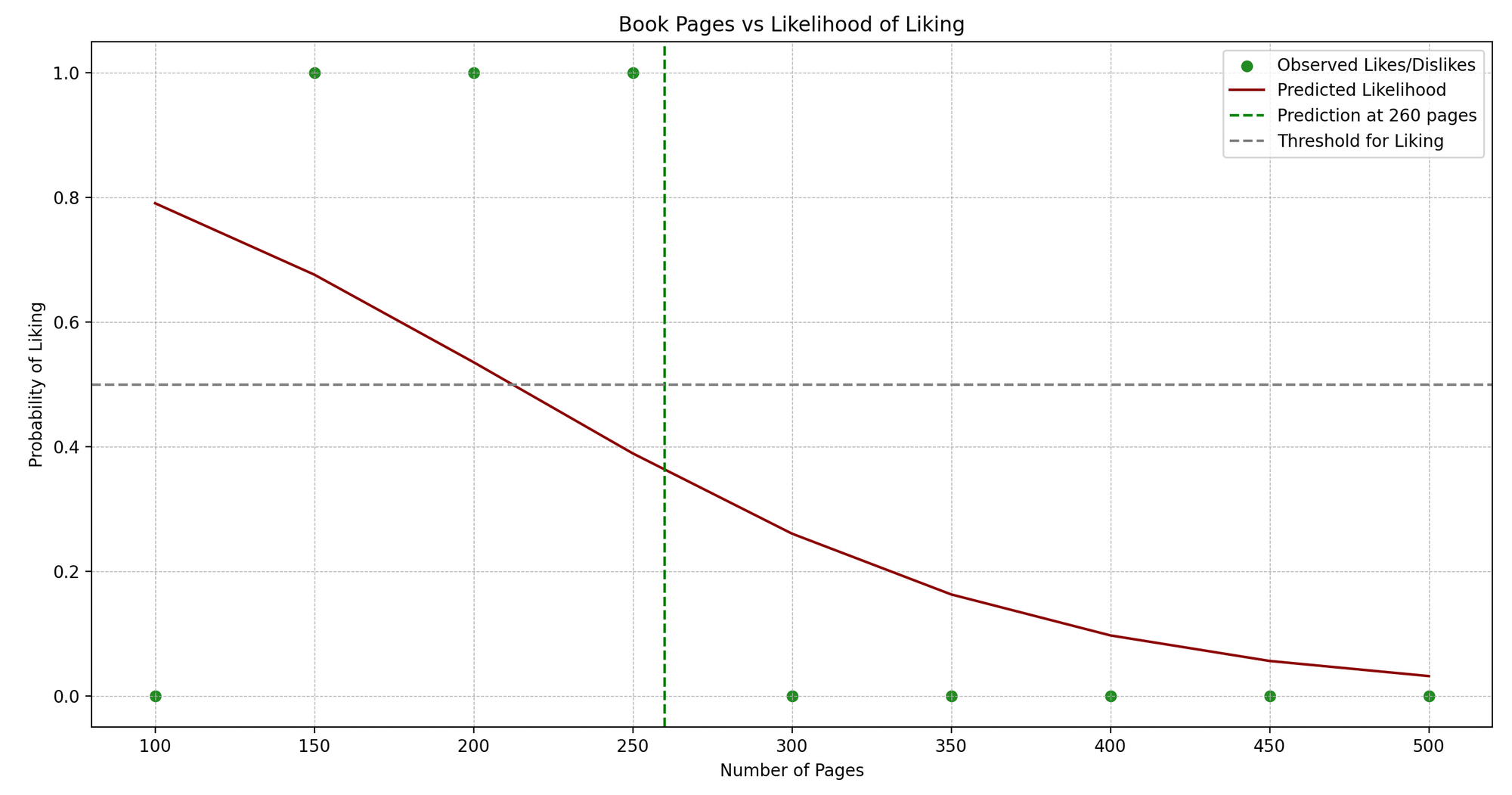
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import LogisticRegressionfrom sklearn.metrics import accuracy_score#样本数据pages = np.array([100, 150, 200, 250, 300, 350, 400, 450, 500]).reshape(-1, 1)likes = np.array([0, 1, 1, 1, 0, 0, 0, 0, 0]) # 1:喜欢,0:不喜欢#创建逻辑回归模型model = LogisticRegression()#训练模型model.fit(pages, likes)#预测predict_book_pages = 260predicted_like = model.predict([[predict_book_pages]])#绘图plt.scatter(pages, likes, color='forestgreen')plt.plot(pages, model.predict_proba(pages)[:, 1], color='darkred')plt.title('书页数 vs 喜欢/不喜欢')plt.xlabel('页数')plt.ylabel('喜欢程度')plt.axvline(x=predict_book_pages, color='green', linestyle='--')plt.axhline(y=0.5, color='grey', linestyle='--')plt.show()#显示预测print(f"Jenny会 {'喜欢' if predicted_like[0] == 1 else '不喜欢'}页数为{predict_book_pages}的书。")- 样本数据:
pages表示Jenny阅读的书籍的页数,likes表示她是否喜欢(1表示喜欢,0表示不喜欢)。 - 创建和训练模型:我们实例化
LogisticRegression()并使用.fit()来训练我们的模型。 - 预测:我们预测Jenny是否会喜欢一本具有特定页数的书(在此示例中为260页)。
- 绘图:我们可视化原始数据点(蓝色)和预测的概率曲线(红色)。绿色虚线表示我们在预测的页面数量,灰色虚线表示阈值(0.5)在此之上我们预测为“喜欢”。
- 显示预测:我们根据我们模型的预测输出Jenny是否会喜欢给定页数的书。

2.3 线性判别分析(LDA)
另一种分类技术与逻辑回归密切相关,称为线性判别分析(LDA)。逻辑回归通常用于建模观测属于具有2个类别的结果变量的概率,而LDA通常用于建模观测属于具有3个及以上类别的结果变量的概率。
LDA提供了一种替代方法来建模条件概率,给定一组预测变量,可以解决逻辑回归的问题。它在每个响应类别(即给定 Y )中分别建模预测变量 X 的分布,然后使用贝叶斯定理将这两者转换为对 Pr(Y = k|X = x) 的估计。
请注意,在LDA的情况下,这些分布被假定为正态分布。事实证明,该模型在形式上与逻辑回归非常相似。在这个方程中:
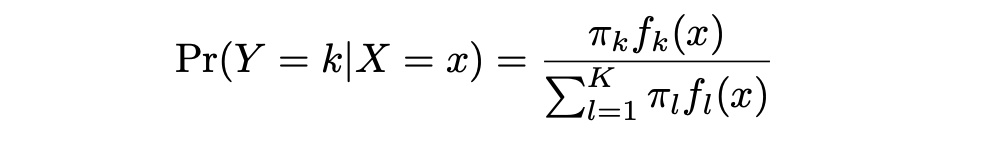
π_k 表示随机选择的观测来自第 k 类的总体先验概率。f_k(x),等于 Pr(X = x|Y = k),表示观测来自第 k 类的具有特定预测变量 X 的后验概率,表示预测变量的密度函数。
这是在观测来自特定类别的情况下,X=x 的概率。换句话说,它是观测属于第 k 类别的概率,给定该观测的预测变量值。
假设 f_k(x) 符合正态或高斯分布,正态密度函数采取以下形式(这是单个维度的情况):
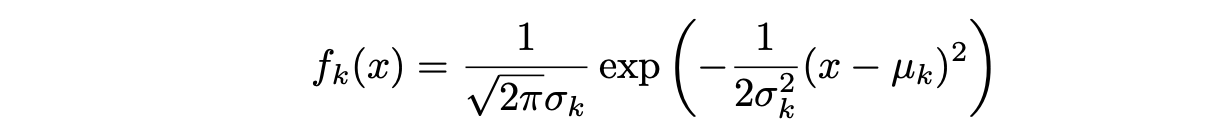
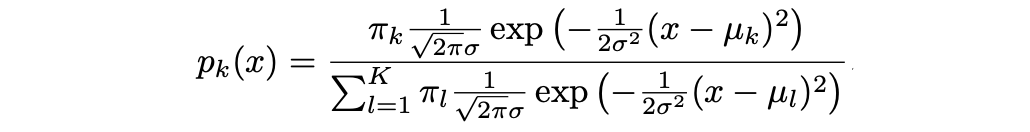
其中 μ_k 和 σ_k² 是第 k 类的均值和方差参数。 假设 σ_¹² = · · · = σ_K²(在所有 K 类中共享方差项,我们用 σ2 表示)。
然后,LDA使用以下对 πk,μk 和 σ2 的估计来近似贝叶斯分类器:
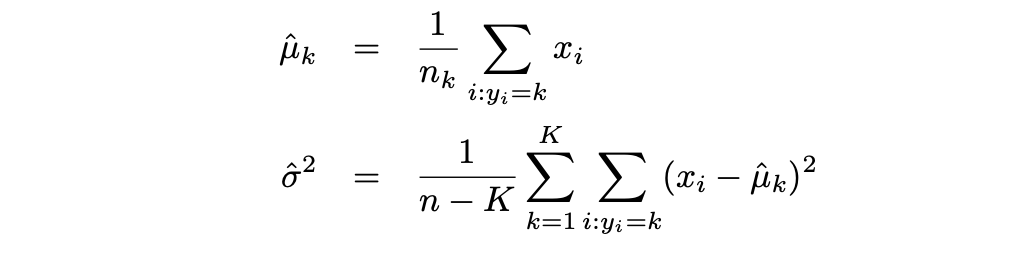
逻辑回归通常用于建模观测属于具有2个类别的结果变量的概率,而LDA通常用于建模观测属于具有3个及以上类别的结果变量的概率。
2.3.1 Python 中的线性判别分析
想象一下,喜欢烹饪和尝试各种水果的莎拉。她发现她喜欢的水果通常具有特定的大小和甜度水平。
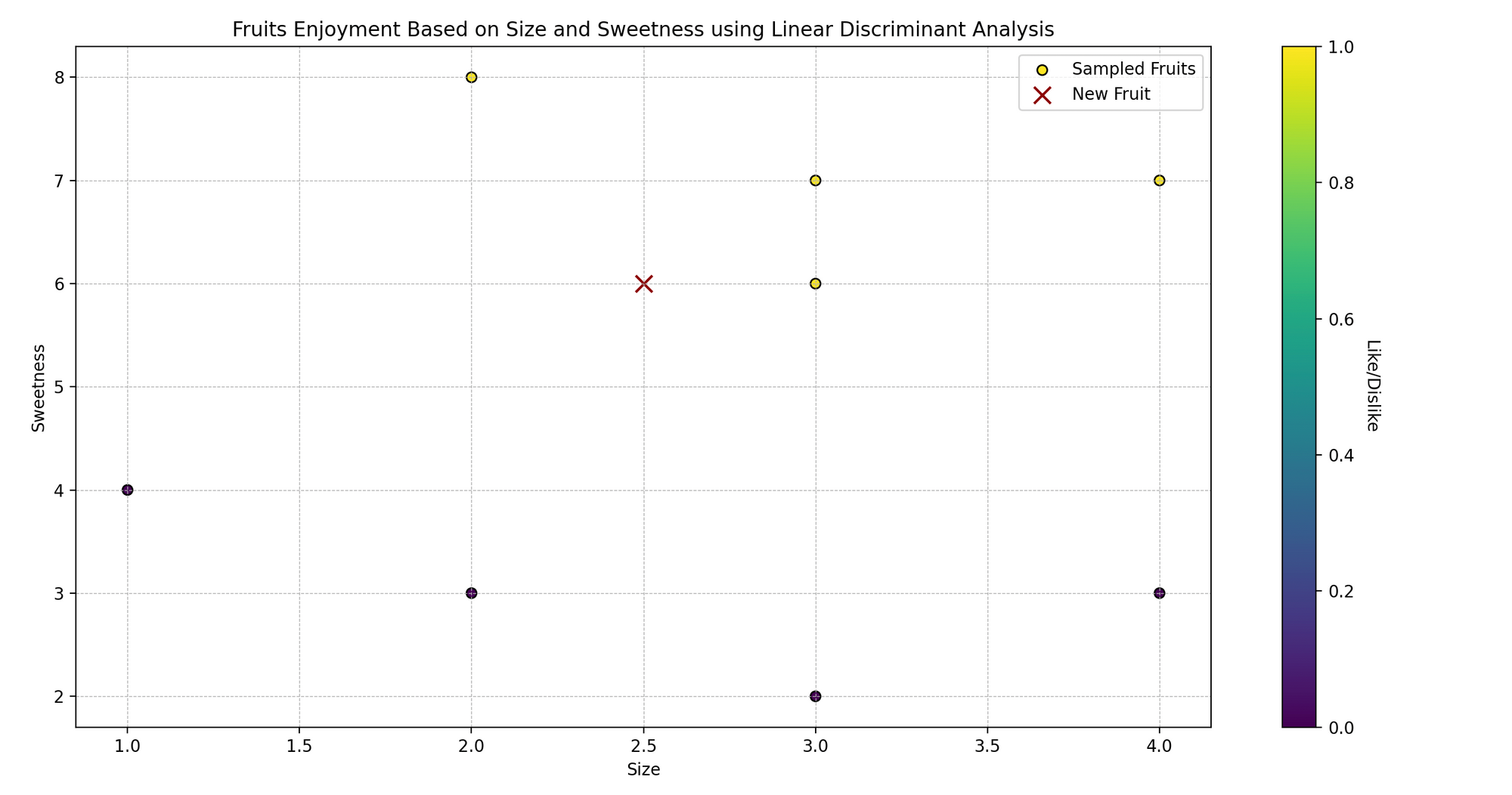
现在,莎拉好奇:她可以根据水果的大小和甜度预测她是否会喜欢它吗?让我们使用线性判别分析(LDA)帮助她预测她是否会喜欢某种水果。
在技术语言中,我们试图根据两个预测变量(大小和甜度)对水果进行分类(喜欢/不喜欢)。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# 样本数据
# [大小, 甜度]
fruits_features = np.array([[3, 7], [2, 8], [3, 6], [4, 7], [1, 4], [2, 3], [3, 2], [4, 3]])
fruits_likes = np.array([1, 1, 1, 1, 0, 0, 0, 0]) # 1: 喜欢, 0: 不喜欢
# 创建LDA模型
model = LinearDiscriminantAnalysis()
# 训练模型
model.fit(fruits_features, fruits_likes)
# 预测
new_fruit = np.array([[2.5, 6]]) # [大小, 甜度]
predicted_like = model.predict(new_fruit)
# 绘图
plt.scatter(fruits_features[:, 0], fruits_features[:, 1], c=fruits_likes, cmap='viridis', marker='o')
plt.scatter(new_fruit[:, 0], new_fruit[:, 1], color='darkred', marker='x')
plt.title('基于大小和甜度的水果喜好')
plt.xlabel('大小')
plt.ylabel('甜度')
plt.show()
# 显示预测结果
print(f"Sarah将 {'喜欢' if predicted_like[0] == 1 else '不喜欢'} 大小为 {new_fruit[0, 0]} 和甜度为 {new_fruit[0, 1]} 的水果。")- 样本数据:
fruits_features包含水果的大小和甜度两个特征,fruits_likes表示Sarah是否喜欢这些水果(1表示喜欢,0表示不喜欢)。 - 创建和训练模型: 我们实例化
LinearDiscriminantAnalysis()并使用样本数据进行训练.fit()。 - 预测: 我们预测Sarah是否喜欢具有特定大小和甜度水平的水果(在这个例子中为[2.5, 6])。
- 绘图: 我们将原始数据点可视化,根据Sarah的喜好(黄色为喜欢,紫色为不喜欢)进行着色,并用红色的“x”标记新水果。
- 显示预测结果: 我们根据模型的预测输出,显示Sarah是否喜欢具有给定大小和甜度水平的水果。
2.4 逻辑回归 vs LDA
逻辑回归是一种常用的二分类方法。但是当类别之间有明显分离或类别数超过2时,逻辑回归模型的参数估计结果会出现意外不稳定。
与逻辑回归不同,当类别数超过2时LDA不会遇到这个不稳定性问题。如果样本数量较小,并且预测变量X在各个类别中近似服从正态分布,LDA相比逻辑回归模型再次更稳定。
2.5 朴素贝叶斯
另一种依赖贝叶斯定理(如LDA)的分类方法是朴素贝叶斯分类。关于贝叶斯定理、贝叶斯规则及相应实例的更多内容,你可以阅读这些 文章。
像逻辑回归一样,你可以使用朴素贝叶斯方法对观测进行二分类(0或1)。
该方法的思想是计算观测属于某一类别的概率,给定该类别的先验概率和给定类别的每个特征值的条件概率。具体而言:
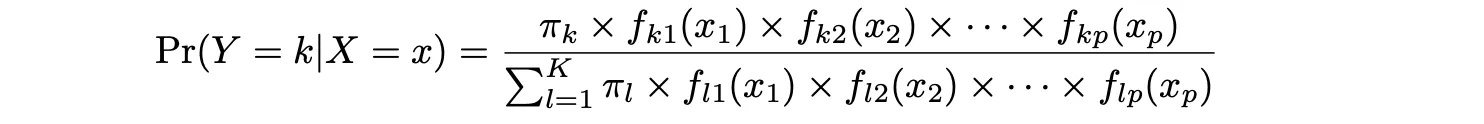
其中Y表示观测的类别,k为第k个类别,x1, …, xn分别表示特征1到特征n。f_k(x) = Pr(X = x|Y = k)表示后验概率,类似于LDA的情况下观测来自第k个类别的变量的密度函数。
如果你将上述表达式与你在LDA中看到的表达式进行比较,你会发现一些相似之处。
在LDA中,我们为了简化目的作出了一个非常重要且强大的假设:即f_k是具有类特定均值μ_k和共享协方差矩阵Sigma Σ的多元正态随机变量的密度函数。
这个假设有助于将估计K个p维密度函数的非常具有挑战性的问题替换为更简单的问题,即估计K个p维均值向量和一个(p×p)维协方差矩阵。
在朴素贝叶斯分类器的情况下,它使用了不同的方法来估计f_1(x), …, f_K(x)。我们不假设这些函数属于特定的分布族(例如正态分布或多元正态分布),而是做出一个单一的假设:在第k类中,p个预测变量是独立的。也就是说:
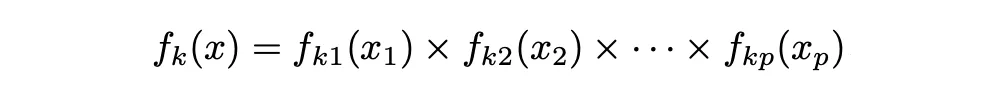
因此,贝叶斯分类器假设特定变量或特征的值在给定类/标签变量的情况下与任何其他变量的值无关(不相关)。
例如,如果一个水果是黄色的、椭圆形的,长度约为5-10厘米,那么它可能被认为是一个香蕉。因此,朴素贝叶斯分类器认为这些不同的水果特征对于确定该水果是香蕉的概率有独立的贡献,而不考虑颜色、形状和长度特征之间的任何可能相关性。
朴素贝叶斯估计
与逻辑回归类似,在朴素贝叶斯分类方法中,我们使用最大似然估计(MLE)作为估计技术。这里有一篇提供了详细而简明的总结,并附有对应示例的文章,你可以在这里找到。
2.5.1 Python中的朴素贝叶斯
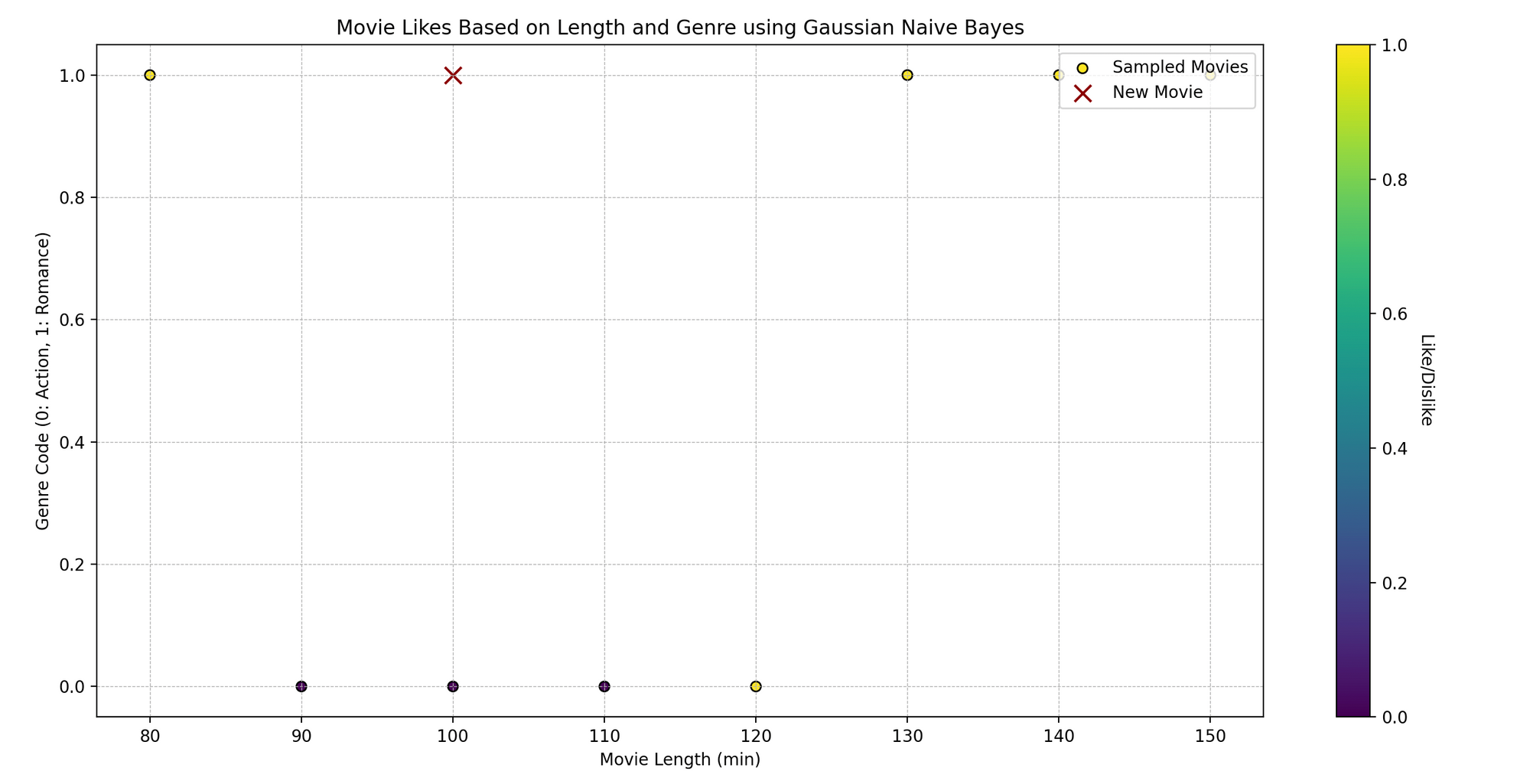
Tom是一个电影爱好者,他观看不同类型的电影并记录他对电影的反馈——喜欢与否。他注意到他是否喜欢一部电影可能取决于两个方面:电影的长度和它的类型。我们能否根据这两个特征预测Tom是否会喜欢一部电影,使用朴素贝叶斯方法呢?
从技术上讲,我们希望根据独立变量(电影长度和类型)来预测二进制结果(喜欢/不喜欢)。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.naive_bayes import GaussianNB# 样本数据# [电影长度, 类型编码](假设类型编码为:0表示动作片,1表示浪漫片,等等)movies_features = np.array([[120, 0], [150, 1], [90, 0], [140, 1], [100, 0], [80, 1], [110, 0], [130, 1]])movies_likes = np.array([1, 1, 0, 1, 0, 1, 0, 1]) # 1: 喜欢, 0: 不喜欢# 创建朴素贝叶斯模型model = GaussianNB()# 训练模型model.fit(movies_features, movies_likes)# 预测new_movie = np.array([[100, 1]]) # [电影长度, 类型编码]predicted_like = model.predict(new_movie)# 绘图plt.scatter(movies_features[:, 0], movies_features[:, 1], c=movies_likes, cmap='viridis', marker='o')plt.scatter(new_movie[:, 0], new_movie[:, 1], color='darkred', marker='x')plt.title('基于长度和类型的电影喜好')plt.xlabel('电影长度(分钟)')plt.ylabel('类型编码')plt.show()# 显示预测结果print(f"根据我们的模型预测,Tom会{'喜欢' if predicted_like[0] == 1 else '不喜欢'}一部时长为{new_movie[0, 0]}分钟,类型编码为{new_movie[0, 1]}的电影。")- 样本数据:
movies_features包含两个特征:电影长度和类型(以数字编码),而movies_likes表示Tom对它们的喜好(1表示喜欢,0表示不喜欢)。 - 创建和训练模型:我们实例化
GaussianNB()(假设数据服从高斯分布的朴素贝叶斯分类器)并使用我们的数据进行训练.fit()。 - 预测:我们预测Tom是否会喜欢一部新电影,给定其长度和类型编码(在本例中为[100, 1])。
- 绘图:我们将原始数据点可视化,根据Tom的喜好进行颜色编码(黄色表示喜欢,紫色表示不喜欢)。红色的 ‘x’ 代表新电影。
- 显示预测结果:我们打印根据我们的模型预测,Tom是否会喜欢给定长度和类型编码的电影。
2.6 朴素贝叶斯 vs 逻辑回归
朴素贝叶斯分类器已被证明速度更快,具有较高的偏差和较低的方差。逻辑回归具有较低的偏差和较高的方差。根据个人情况和偏差-方差权衡,您可以选择相应的方法。
2.7 决策树
决策树是一种监督和非参数的机器学习方法,用于分类和回归目的。其思想是通过从数据预测器学习简单的决策规则来创建一个预测目标变量值的模型。
与线性回归或逻辑回归不同,决策树是简单且有用的模型选择,当独立变量与因变量之间的关系被认为是非线性时。
基于树的方法将预测空间划分为较小的区域或段。构建决策树的思想是将预测空间划分为不同且互斥的区域 X1,X2,….. ,Xp → R_1,R_2, …,R_N,其中这些区域的形式为框或矩形。通过递归二分分割来找到这些区域,因为最小化残差平方和不可行。这种方法常常被称为贪婪方法。
决策树通过自上而下的分割构建。因此,在开始时,所有观测值属于一个单一区域。然后,模型逐步划分预测空间。每个分割通过树上进一步延伸的两个新分支来指示。
该方法有时被称为贪婪,因为在树构建过程的每个步骤中,都会在该特定步骤中进行最佳分割,而不是展望未来并选择会导致更好决策树的分割。
停止准则
在构建决策树时,通常使用一些常见的停止准则:
- 叶子节点中的最小观察数量。
- 用于节点分割的最小样本数。
- 树的最大深度(纵向深度)。
- 终端节点的最大数量。
- 考虑用于分割的最大特征数量。

例如,重复此分割过程直到没有区域包含超过100个观察值。让我们深入了解一下
1. 叶子节点中的最小观察数量:如果拟议的分割导致叶子节点中的观察数量少于定义的数量,则可能丢弃该分割。这样可以防止树过于复杂。
2. 用于节点分割的最小样本数:要进行节点分割,节点必须至少具有此数量的样本。这确保有足够量的数据来证明分割的合理性。
3. 树的最大深度(纵向深度):限制树可以进行分割的次数。这类似于告诉树在做出决策之前可以问多少个关于数据的问题。
4. 终端节点的最大数量:这是树可以有的末端节点(或叶子)的总数。
5. 考虑用于分割的最大特征数量:对于每个分割,算法仅考虑特征的子集。这可以加快训练速度并有助于泛化。
在构建决策树时,特别是处理大量特征时,树可能会变得过大,叶子过多。这将影响模型的可解释性,并可能导致过拟合 问题。因此,选择一个好的停止准则对于模型的解释性和性能至关重要。
RSS/Gini指数/熵/节点纯度
在构建决策树时,我们使用 RSS(用于回归树)和Gini指数/熵(用于分类树)来选择划分区域的预测器和值。Gini指数和熵经常被称为节点纯度度量,因为它们描述了决策树叶子节点的纯度。
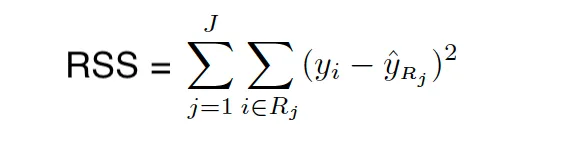
Gini指数
Gini指数测量了K类别之间的总方差。当所有类别的误差率为1或0时,Gini指数取较小的值。这也是为什么它被称为节点纯度的指标 – 当决策树节点主要包含来自同一类别的观测时,Gini指数取较小的值。
Gini指数的定义如下:
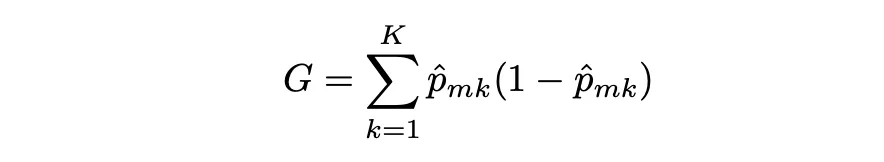
其中,pˆmk表示第m个区域中来自第k个类别的训练观测的比例。
熵
熵是另一个节点纯度的度量指标,与Gini指数类似,如果第m个节点纯净,熵的值也会很小。实际上,Gini指数和熵在数值上非常相似,可以表示如下:
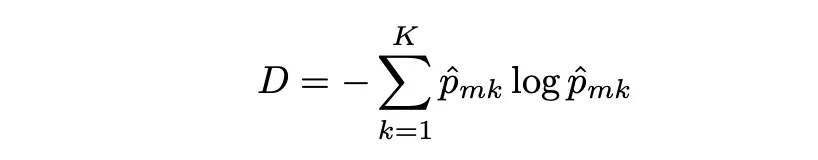
决策树分类示例
让我们看一个示例,其中有三个特征描述消费者过去的行为:
- Recency (顾客最近一次购买是多久之前?)
- Monetary (顾客在一定期间内花了多少钱?)
- Frequency (顾客在一定期间内购买了多少次?)
我们将使用决策树的分类版本,根据描述顾客行为的特征将顾客分到3个类别中(Good:1,Better:2和Best:3)。
在下面的树中,我们使用Gini指数作为纯度度量,我们可以看到第一个最重要的特征是Recency。让我们看一下这棵树,然后解释一下:
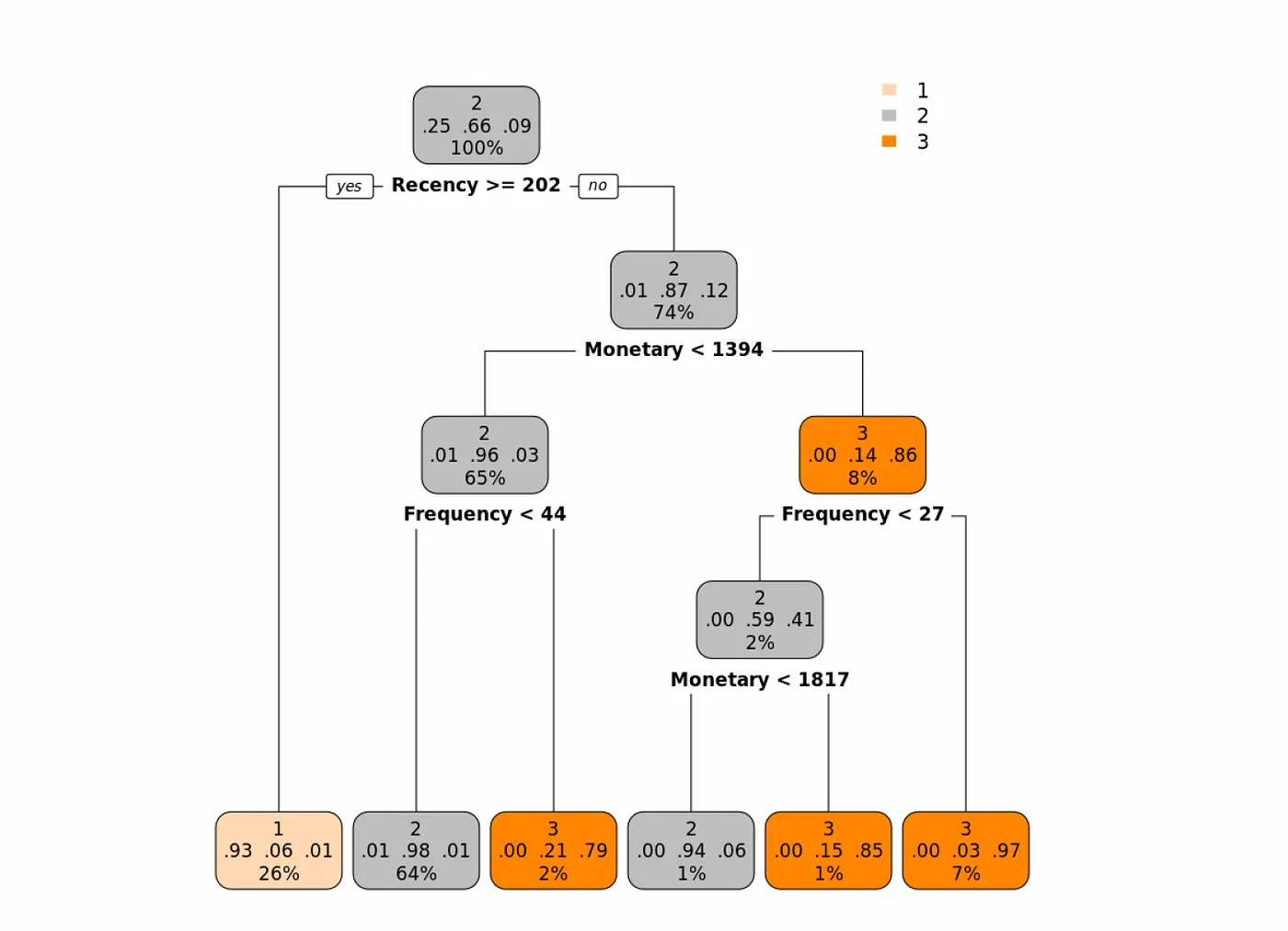
当Recency大于等于202(最后一次购买距今日子大于202天)时,被分配到类别1的概率是93%(基本上,我们可以将这些顾客标记为Good Class)。
对于Recency小于202的顾客(最近购买过),我们查看他们的Monetary值,如果小于1394,则查看他们的Frequency。如果Frequency小于44,我们可以将这些顾客的类别标记为Better(类别2)。依此类推。
决策树Python实现
Alex对学习小时数和学生得分之间的关系感到好奇。Alex从同学那里收集了关于他们学习小时数和相应考试成绩的数据。
他想知道:我们能否根据学习小时数预测学生的成绩?让我们利用决策树回归模型来揭示这个问题。
从技术上讲,我们根据一个自变量(学习小时数)来预测一个连续的结果(考试成绩)。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.tree import DecisionTreeRegressor, plot_tree# 样本数据# [学习小时数]study_hours = np.array([1, 2, 3, 4, 5, 6, 7, 8]).reshape(-1, 1)test_scores = np.array([50, 55, 70, 80, 85, 90, 92, 98])# 创建一个决策树回归模型model = DecisionTreeRegressor(max_depth=3)# 训练模型model.fit(study_hours, test_scores)# 预测new_study_hour = np.array([[5.5]]) # 学习小时数的示例predicted_score = model.predict(new_study_hour)# 绘制决策树plt.figure(figsize=(12, 8))plot_tree(model, filled=True, rounded=True, feature_names=["学习小时数"])plt.title('决策树回归器树')plt.show()# 绘制学习小时数与考试成绩plt.scatter(study_hours, test_scores, color='darkred')plt.plot(np.sort(study_hours, axis=0), model.predict(np.sort(study_hours, axis=0)), color='orange')plt.scatter(new_study_hour, predicted_score, color='green')plt.title('学习小时数与考试成绩')plt.xlabel('学习小时数')plt.ylabel('考试成绩')plt.grid(True)plt.show()# 显示预测结果print(f"对于学习小时数为{new_study_hour[0, 0]}的预测考试成绩为:{predicted_score[0]:.2f}。")- 样本数据:
study_hours包含学习小时数,test_scores包含对应的测试分数。 - 创建和训练模型: 我们使用指定的最大深度(以防止过拟合)创建一个
DecisionTreeRegressor,并使用我们的数据进行训练,使用.fit()方法。 - 绘制决策树:
plot_tree帮助可视化模型的决策过程,表示基于学习小时的拆分。 - 预测和绘制: 我们预测新的学习小时值(在这个例子中为 5.5),可视化原始数据点、决策树的预测分数以及新的预测结果。
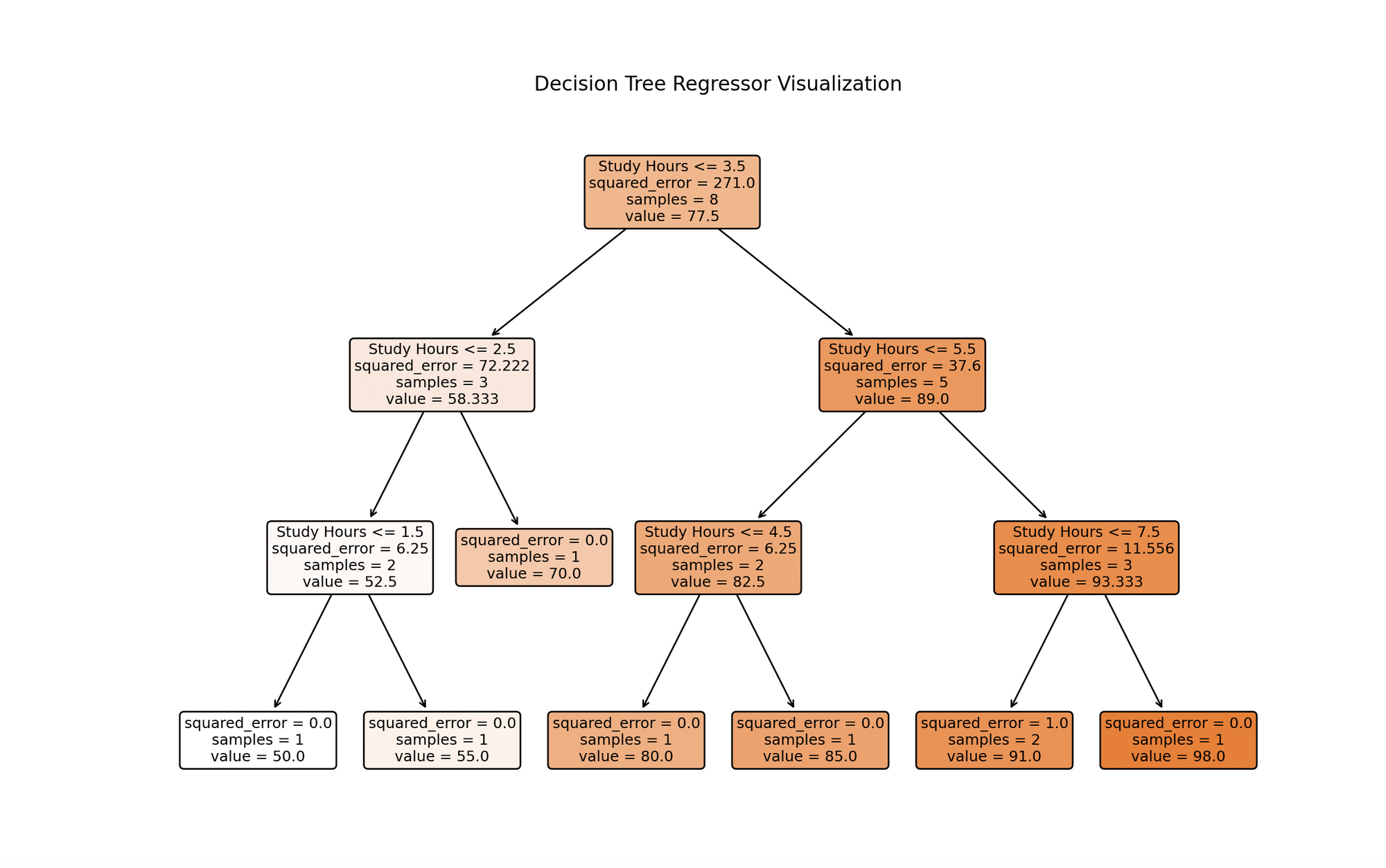
这个可视化展示了一个基于学习小时数据进行训练的决策树模型。每个节点表示基于学习小时的决策,在满足最佳预测测试分数条件的情况下从根节点开始分支。这个过程一直进行,直到达到最大深度或没有更多有意义的拆分。底部的叶节点给出最终的预测值,对于回归树来说,它们是达到该叶节点的训练实例的目标值的平均值。这个可视化突出了模型的预测方法以及学习小时对测试分数的重要影响。
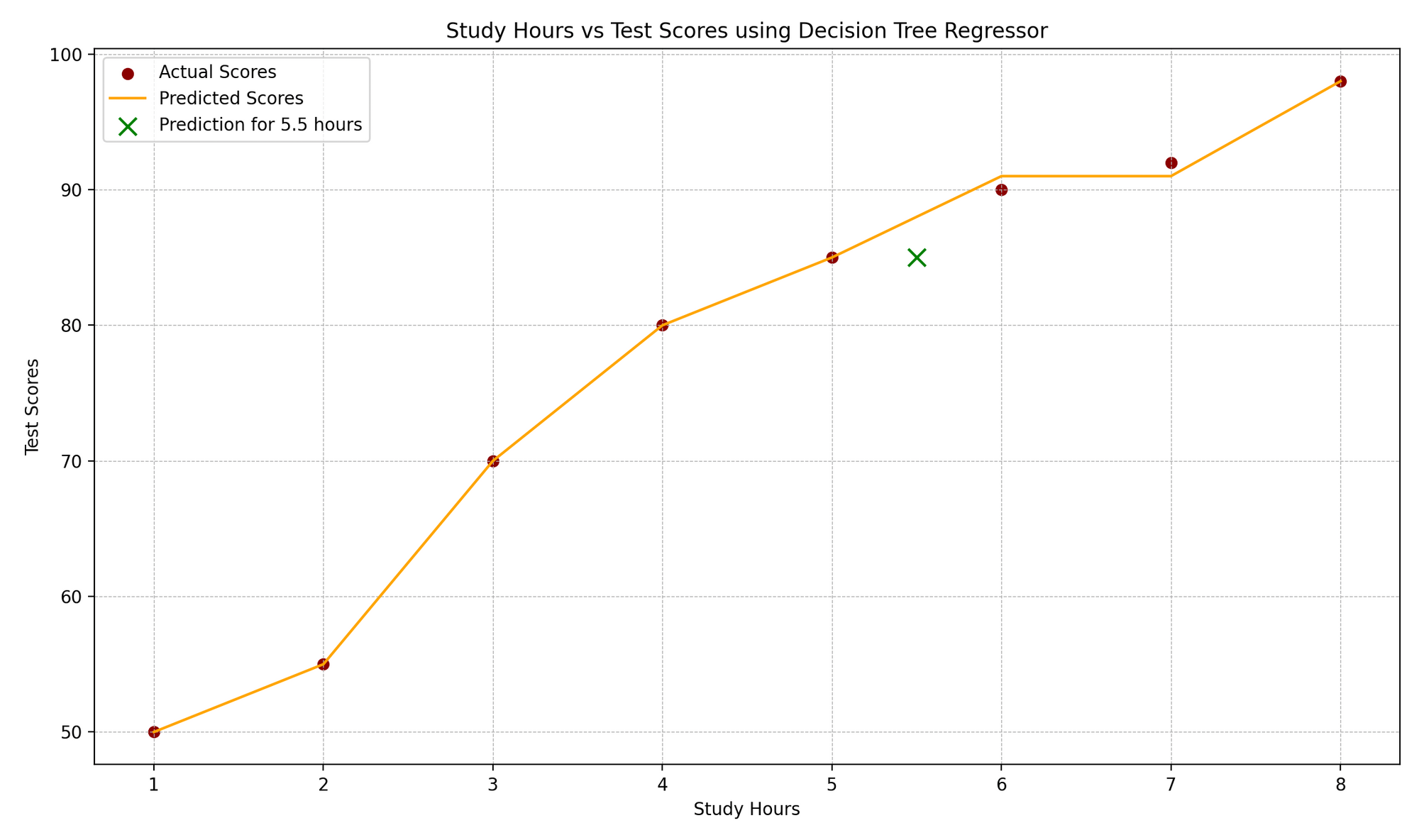
这个”学习小时与测试分数”的图表描绘了学习小时和对应的测试分数之间的相关性。红点表示实际数据点,而模型的预测结果以橙色阶梯函数的形式显示,这是回归树的特征。绿色的”x”标记突出了一个新数据点的预测,这里表示一个持续时间为 5.5 小时的学习。图表的设计元素,如网格线、标签和图例,增强了对真实值与预期值的理解。

2.8 Bagging
决策树的最大缺点之一是它们具有很高的方差。你可能会得到一个容易解释但误导性的模型和预测结果。这会导致做出不正确的结论和业务决策。
因此,为了减小决策树的方差,可以使用一种称为 Bagging 的方法。要理解 Bagging 是什么,你需要了解两个术语:
- 自助法(Bootstrapping)
- 中心极限定理(CLT)
有关 Boostrapping 的更多信息,可以在本手册的后面部分找到。目前,你可以将 Bootstrapping 看作是一种从原始数据中有放回地进行采样的技术,从而创建一个与原始数据非常相似但并不完全相同的副本。
Bagging 也基于中心极限定理的相同思想,该定理是统计学中最重要的定理之一,如果你取多个样本的平均值,那么方差会明显降低,与每个单独样本模型的方差相比。
因此,对于一组独立观测值 Z1,…,Zn,每个观测值的方差为 σ2,观测值均值 Z ̄ 的方差为σ2/n。因此,取多个观测值的平均值可以降低方差。
有关更多统计学细节,请参考以下教程:
 Tatev Karen AslanyanLunarTech
Tatev Karen AslanyanLunarTech
Bagging基本上是使用被采样的Bootstrap来构建B 树的Bootstrap合并方法。通过从单个训练数据中重复采样,Bagging可以用来提高精度(降低多种方法的方差)。
因此,在Bagging中,我们生成B个Bootstrap训练样本,基于这些样本构建B个相似的树(相关的树),这些树最终被合并以计算预测值,因此对这B个样本的预测值取平均。值得注意的是,每棵树都是基于一个独立于其他树的Bootstrap数据集构建的。
因此,在Bagging中,每个树的分裂都考虑了所有的p个特征,这导致了相似的树,因为每次最强的预测变量都在顶部,较弱的预测变量都在底部,结果是所有的袋装树看起来非常相似。
2.8.1 回归树中的Bagging
要将Bagging应用于回归树,我们只需要使用B个Bootstrap训练集构建B个回归树,并对结果进行平均。这些树被深度生长,并且不进行修剪。因此,每棵单独的树具有很高的方差,但偏差很低。将这B个树进行平均可以减少方差。
2.8.2 分类树中的Bagging
对于给定的测试观测,我们可以记录B个树预测的类别,并进行多数票投票:总体预测是在B个预测中最常出现的多数类别。
2.8.3 OOB(袋外)误差估计
当Bagging应用于决策树时,不再需要应用交叉验证来估计测试错误率。在Bagging中,我们重复地将树与Bootstrap样本拟合 – 平均只有其中2/3的观测值被使用。其他1/3在训练过程中不被使用。这些被称为袋外观测。
因此,每个观测值共有B/3的预测结果在训练中未被使用。我们可以对这些情况下(或多数类别)的响应值取平均值。因此,每个观测值的OOB误差和这些平均值形成了测试错误率。
2.8.4 Python中的Bagging
这里有一个名叫Lucy的健身教练,她想根据客户每日卡路里摄入量和锻炼时间来预测他们的减肥情况。Lucy拥有过去客户的数据,但意识到个体预测可能存在误差。让我们利用Bagging来创建一个更稳定的预测模型。
从技术上讲,我们将基于独立变量(每日卡路里摄入量和锻炼时间)使用Bagging来预测一个连续的结果(减肥情况),以减少预测中的方差。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import BaggingRegressor
from sklearn.tree import DecisionTreeRegressor, plot_tree
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 样本数据
clients_data = np.array([[2000, 60], [2500, 45], [1800, 75], [2200, 50], [2100, 62], [2300, 70], [1900, 55], [2000, 65]])
weight_loss = np.array([3, 2, 4, 3, 3.5, 4.5, 3.7, 4.2])
# 训练集和测试集划分
X_train, X_test, y_train, y_test = train_test_split(clients_data, weight_loss, test_size=0.25, random_state=42)
# 创建Bagging模型
base_estimator = DecisionTreeRegressor(max_depth=4)
model = BaggingRegressor(base_estimator=base_estimator, n_estimators=10, random_state=42)
# 训练模型
model.fit(X_train, y_train)
# 预测和评估
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
# 显示预测和评估结果
print(f"True weight loss: {y_test}")
print(f"Predicted weight loss: {y_pred}")
print(f"Mean Squared Error: {mse:.2f}")
# 可视化其中一个基础估算器(如果需要)
plt.figure(figsize=(12, 8))
tree = model.estimators_[0]
plt.title('One of the Base Decision Trees from Bagging')
plot_tree(tree, filled=True, rounded=True, feature_names=["Calorie Intake", "Workout Duration"])
plt.show()
True weight loss: [2. 4.5]
Predicted weight loss: [3.1 3.96]
Mean Squared Error: 0.75
- 样本数据:
clients_data包含每日卡路里摄入量和锻炼时长,weight_loss包含相应的减重数据。 - 训练-测试拆分:我们将数据拆分为训练集和测试集,以验证模型的预测性能。
- 创建和训练模型:我们使用
BaggingRegressor实例化,并使用.fit()函数训练使用训练数据的DecisionTreeRegressor基估计器。 - 预测和评估:我们对测试数据进行减重预测,并使用均方误差(MSE)评估预测质量。
- 可视化一个基估计器:按需可视化集合中的一棵树,以了解个别的决策过程(但要记住个别树可能表现不佳,但集体上它们产生稳定的预测)。
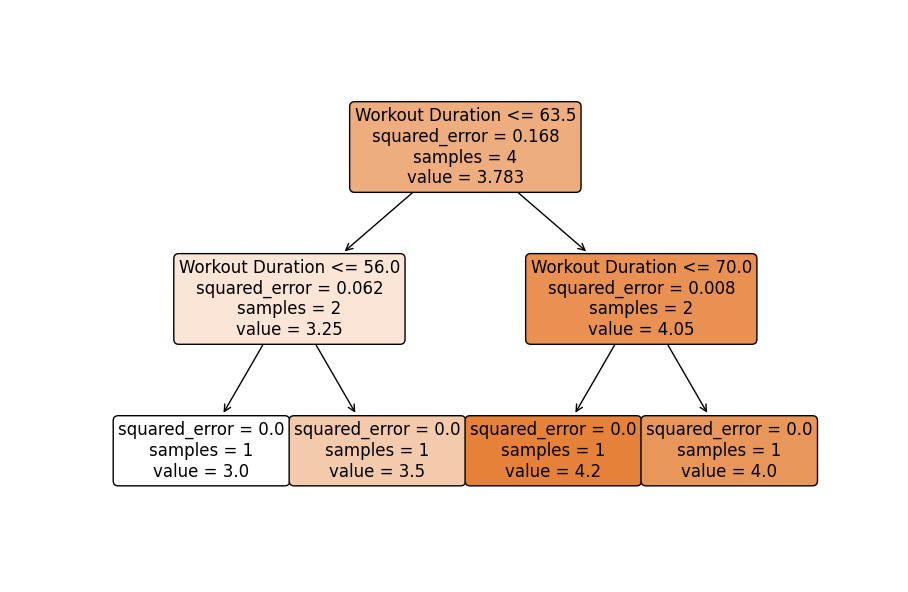
2.9 随机森林
随机森林通过对树进行微小调整来改进装袋树的性能。
与装袋相同,我们在自助训练样本上构建多棵决策树。但是,在构建这些决策树时,每次考虑树中的一个分割时,从 p 个预测变量集中选择 m 个预测变量作为分割候选项。
分割仅允许使用那 m 个预测变量之一。在每个分割点都会重新随机选择 m 个预测变量,并且通常我们选择 m ≈ √p – 也就是说,每次分割时考虑的预测变量数量大约等于总预测变量数量的平方根。这也是随机森林被称为 “random” 的原因。
装袋和随机森林之间的主要区别在于选择预测变量子集大小的方式, m 能够使树之间更不相关。
在存在大量相关预测变量的情况下,使用较小的 m 值构建随机森林通常会很有帮助。因此,如果你遇到多重共线性问题,随机森林是解决该问题的好方法。
因此,不同于装袋,对于随机森林来说,在每个树的分割中并不考虑所有 p 个预测变量,而是只从中随机选择 m 个预测变量。这样将导致不同的树之间不相关。由于平均不相关的树会导致更小的方差,随机森林比装袋更准确。
2.9.1 随机森林 Python 实现
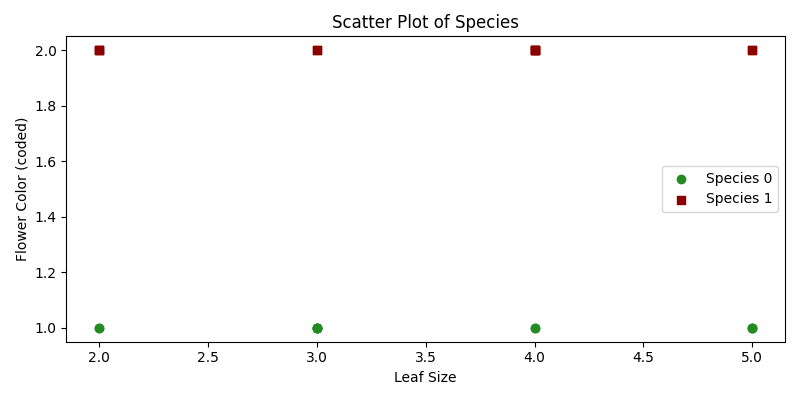
Noah 是一位植物学家,他收集了各种植物物种以及它们的特征数据,例如叶片大小和花朵颜色。Noah 想知道是否可以根据这些特征预测植物的物种。
在这里,我们将利用随机森林这种集成学习方法来帮助他对植物进行分类。
从技术上讲,我们目标是使用随机森林模型基于某些预测变量对植物物种进行分类。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.ensemble import RandomForestClassifierfrom sklearn.model_selection import train_test_splitfrom sklearn.metrics import classification_report# 扩展的数据集plants_features = np.array([ [3, 1], [2, 2], [4, 1], [3, 2], [5, 1], [2, 2], [4, 1], [5, 2], [3, 1], [4, 2], [5, 1], [3, 2], [2, 1], [4, 2], [3, 1], [4, 2], [5, 1], [2, 2], [3, 1], [4, 2], [2, 1], [5, 2], [3, 1], [4, 2]])plants_species = np.array([ 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1])# 训练-测试拆分X_train, X_test, y_train, y_test = train_test_split(plants_features, plants_species, test_size=0.25, random_state=42)# 创建随机森林模型model = RandomForestClassifier(n_estimators=10, random_state=42)# 训练模型model.fit(X_train, y_train)# 预测和评估y_pred = model.predict(X_test)classification_rep = classification_report(y_test, y_pred)# 显示预测和评估结果print("分类报告:")print(classification_rep)# 散点图可视化类别plt.figure(figsize=(8, 4))for species, marker, color in zip([0, 1], ['o', 's'], ['forestgreen', 'darkred']): plt.scatter(plants_features[plants_species == species, 0], plants_features[plants_species == species, 1], marker=marker, color=color, label=f'物种 {species}')plt.xlabel('叶片大小')plt.ylabel('花朵颜色(编码)')plt.title('物种散点图')plt.legend()plt.tight_layout()plt.show()# 可视化特征重要性plt.figure(figsize=(8, 4))features_importance = model.feature_importances_features = ["叶片大小", "花朵颜色"]plt.barh(features, features_importance, color = "darkred")plt.xlabel('重要性')plt.ylabel('特征')plt.title('特征重要性')plt.show()- 样本数据:
plants_features包含叶片大小和花朵颜色,而plants_species表示相应植物的物种。 - 训练-测试拆分:我们将数据分成训练集和测试集。
- 创建和训练模型:我们使用指定数量的树(此处为10)来实例化
RandomForestClassifier,并使用我们的训练数据进行训练。 - 预测与评估:我们对测试数据进行物种预测,并使用分类报告评估预测结果,其中提供精确度、召回率、f1-score 和支持度。
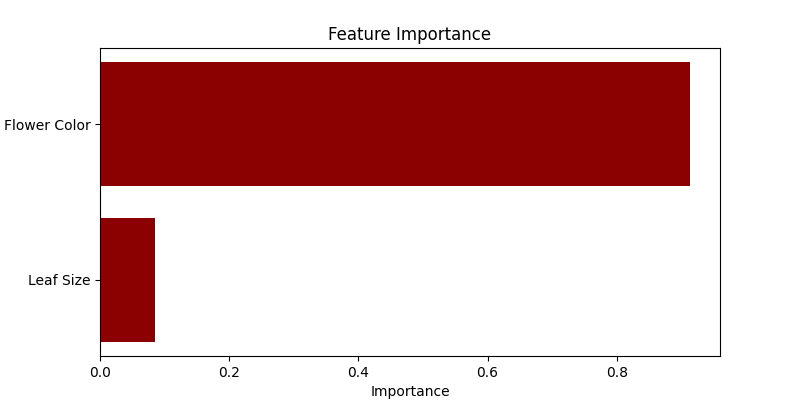
- 可视化特征重要性:我们使用水平条形图显示每个特征在预测植物物种中的重要性。随机森林在构建树的过程中量化特征的有用性,我们在此可视化。

2.10 提升或集成模型
与 Bagging(对相关决策树进行平均)和 Random Forest(对不相关决策树进行平均)一样,提升旨在改善决策树的预测结果。提升是一种用于回归和分类问题的监督式机器学习模型。
与 Bagging 或 Random Forest 不同,在这里,树是依次建立的,并且彼此之间是相互依赖的。每棵树都使用先前建立的树的信息进行生长。
提升不涉及自助采样。相反,每棵树都适合修改后的原始数据集的版本。这是一种将弱学习器转化为强学习器的方法。
在提升中,每棵新树都是对原始数据集的修改版本进行拟合。因此,与将单个大决策树拟合到数据相比,后者将数据拟合得更完整,并可能过拟合,提升方法学习速度较慢。
给定当前模型,我们对模型的残差拟合一棵决策树。也就是说,我们使用当前残差而不是结果 Y 作为响应来拟合一棵树。然后,我们将这棵新决策树添加到适配函数中以更新残差。
这些树中的每一棵都可以相当小,只有几个终端节点,由算法中的参数 d 确定。现在让我们来看一下机器学习中最流行的 3 个提升模型:
- AdaBoost
- GBM
- XGBoost
2.10.1 提升:AdaBoost
今天我们要介绍的第一个集成算法是 AdaBoost。与所有提升技术一样,在 AdaBoost 的情况下,树是使用先前树的信息构建的,更具体地说是使用未执行良好的部分树。这称为弱学习器(决策桩)。此决策桩仅使用单个预测器而不是所有预测器来执行预测。
因此,AdaBoost 将弱学习器组合起来进行分类,每个树桩都是通过使用上一个树桩的错误来构建的。下面是构建 AdaBoost 模型的步骤:
- 步骤 1:初始化权重分配 – 给样本中的所有观测值分配相等的权重。此权重表示正确分类观测值的重要性:1/N (在此阶段,所有样本的重要性都是相等的)。
- 步骤 2:最佳预测器选择 – 第一个树桩通过计算每个预测器的 RSS(在回归的情况下)或 GINI 指数/熵(在分类的情况下)来构建。选择在预测准确性方面表现最好的树桩,即具有最小 RSS 或最小 GINI/熵的树桩。
- 步骤 3:根据树桩总误差计算树桩权重 – 决定这棵树在最终树中的重要性时,使用该树所造成的总误差。如果某个树桩没有比随机抛硬币更好的表现,其总误差为 0.5,则其权重为 0。权重 = 0.5*log(1-总误差/总误差)
- 步骤 4:更新观测权重 – 增加错误预测的观测值的权重,减少具有更高准确性或被正确分类的其他观测值的权重,以便下一个树桩对于正确预测该观测值的值具有更高的重要性。
- 步骤 5:根据更新的权重构建下一个树桩 – 使用加权 Gini 指数选择下一个树桩。
- 步骤 6:组合 B 个树桩 – 将所有树桩组合起来,同时考虑它们的重要性,进行加权求和。
AdaBoost Python实现
想象一种场景,我们根据房屋的某些特征(如房间数量和房龄)来预测房价。
对于这个例子,让我们生成一些合成数据,其中:
num_rooms:房屋的房间数量。
house_age:房屋的年龄(以年为单位)。
price:房屋的价格(以千美元为单位)。
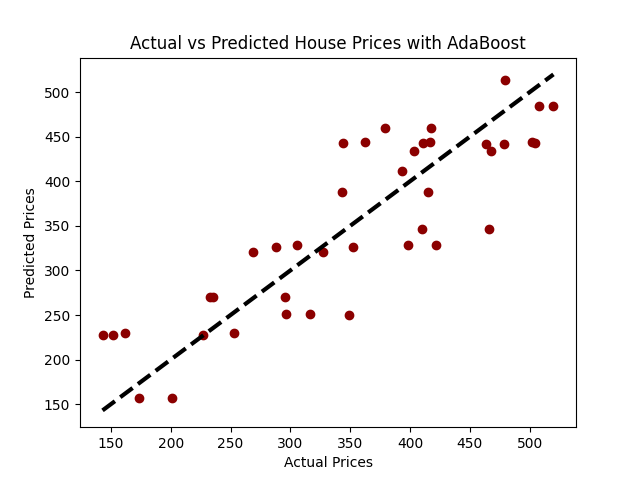
import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn.model_selection import train_test_splitfrom sklearn.ensemble import AdaBoostRegressorfrom sklearn.metrics import mean_squared_error# 为了可重复性设置种子np.random.seed(42)# 生成合成数据num_samples = 200num_rooms = np.random.randint(3, 10, num_samples)house_age = np.random.randint(1, 100, num_samples)noise = np.random.normal(0, 50, num_samples)# 假设价格与房间数量和房龄之间存在线性关系,即 price = 50*rooms + 0.5*age + noiseprice = 50*num_rooms + 0.5*house_age + noise# 创建DataFrame对象data = pd.DataFrame({'num_rooms': num_rooms, 'house_age': house_age, 'price': price})# 绘制散点图plt.scatter(data['num_rooms'], data['price'], label='房间数量 vs 价格', color='forestgreen')plt.scatter(data['house_age'], data['price'], label='房龄 vs 价格', color='darkred')plt.xlabel('特征值')plt.ylabel('价格')plt.legend()plt.title('特征与价格的散点图')plt.show()# 将数据分为训练集和测试集X = data[['num_rooms', 'house_age']]y = data['price']X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 初始化并训练AdaBoost回归模型model_ab = AdaBoostRegressor(n_estimators=100, random_state=42)model_ab.fit(X_train, y_train)# 预测predictions = model_ab.predict(X_test)# 评估模型mse = mean_squared_error(y_test, predictions)rmse = np.sqrt(mse)print(f"均方误差:{mse:.2f}")print(f"均方根误差:{rmse:.2f}")# 可视化:实际价格与预测价格plt.scatter(y_test, predictions, color='darkred')plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=3)plt.xlabel('实际价格')plt.ylabel('预测价格')plt.title('AdaBoost预测的实际价格与预测价格')plt.show()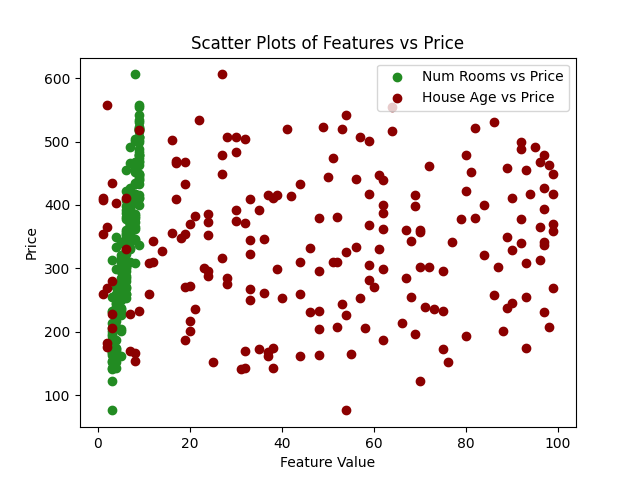
2.10.2 Boosting算法:Gradient Boosting模型(GBM)
AdaBoost和Gradient Boosting非常相似。但与AdaBoost相比,Gradient Boosting从单个叶子节点开始,而不是从树桩开始构建。
选择的叶子节点对应的结果是因变量的初始猜测。与AdaBoost类似,Gradient Boosting使用先前树桩的误差来构建树。但与AdaBoost不同,Gradient Boost构建的树比树桩更大。这是一个参数,我们将其设置为最大叶子节点数。
为了确保树不过拟合,Gradient Boosting使用学习率来缩放梯度贡献。Gradient Boosting基于这样一个思想,即在正确方向上采取许多小步长(梯度)将会降低方差(对测试数据而言)。
AdaBoost和Gradient Boosting算法的主要区别在于它们如何识别弱学习器(例如决策树)的不足之处。AdaBoost模型通过使用高权重数据点来识别不足之处,而梯度提升则通过使用损失函数中的梯度来实现同样的目的(y=ax+b+e,需要特别提及的是误差项e)。
损失函数是衡量模型系数拟合底层数据的好坏度量。对损失函数的逻辑理解取决于我们要优化的目标。
提前停止(Early Stopping)
调整算法迭代次数的特殊过程(如GBM和随机森林)称为“提前停止”-这是我们在讨论决策树时涉及的现象。
提前停止通过监控模型在单独的测试数据集上的性能并在性能在一定的迭代次数后停止改善时停止训练过程,从而执行模型优化。
它避免过拟合,通过试图自动选择性能在测试数据集上开始下降,而在模型开始过拟合时在训练数据集上继续改善的拐点。
在GBM的背景下,提前停止可以基于包外样本集(“OOB”)或交叉验证(“CV”)进行。在前面提到过,停止训练模型的理想时间是在验证错误率下降并开始稳定之前,因为它开始由于过拟合而增加。
构建GBM,按照以下逐步过程进行:
- 步骤1:在现有数据上训练模型以预测结果变量
- 步骤2:使用预测值和实际值计算错误率(伪残差)
- 步骤3:使用现有特征和伪残差作为结果变量再次预测残差
- 步骤4:使用预测的残差更新步骤1的预测,同时使用学习率(超参数)对树进行缩放
- 步骤5:重复步骤1-4,即更新伪残差和树的过程,同时使用学习率进行缩放,直到不再改善或达到停止规则
理念是每次将一个新的缩放树添加到模型中,残差应该变得更小。
在任何m步骤中,梯度提升模型生成的模型是先前步骤F(m-1)和学习率eta与该步骤上模型输出的损失函数的负导数乘积的整体。

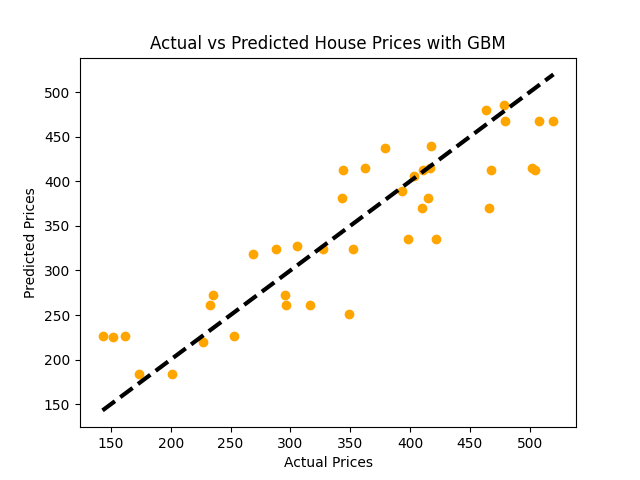
GBM Python实现
# 初始化和训练梯度提升回归模型model_gbm = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1, max_depth=1, random_state=42)model_gbm.fit(X_train, y_train)# 预测predictions = model_gbm.predict(X_test)# 评估模型mse = mean_squared_error(y_test, predictions)rmse = np.sqrt(mse)print(f"均方误差:{mse:.2f}")print(f"均方根误差:{rmse:.2f}")# 可视化:实际与预测价格plt.scatter(y_test, predictions, color = 'orange')plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=3)plt.xlabel('实际价格')plt.ylabel('预测价格')plt.title('使用GBM的实际与预测房价')plt.show()
2.10.3 Boosting算法:XGBoost
最流行的Boosting或Ensemble算法之一是极端梯度提升(XGBoost)。
GBM和XGBoost之间的区别在于XGBoost计算二阶导数(二阶梯度)。这提供了关于梯度方向和如何达到损失函数最小值的更多信息。
请记住,这是为了识别弱学习器并通过改进弱学习器来改进模型。
XGBoost背后的思想是,二阶导数在找到准确方向方面更精确。与AdaBoost类似,XGBoost应用L1或L2范数的高级正则化来解决过拟合问题。
与AdaBoost不同,由于其特殊的缓存机制,XGBoost可以并行化处理大规模和复杂的数据集。此外,为了加快训练速度,XGBoost使用近似贪婪算法,只考虑有限数量的阈值来分裂树的节点。
构建一个XGBoost模型,按照以下步骤进行:
- 步骤1:拟合单个决策树 – 在这一步中,计算损失函数,例如NDCG,以评估模型。
- 步骤2:添加第二棵树 – 这样做的目的是,当将第二棵树添加到模型中时,基于一阶和二阶导数相对于前一棵树降低损失函数(此处使用学习率eta)。
- 步骤3:找到下一步的方向 – 通过使用一阶和二阶导数,我们可以找到使损失函数减少最多的方向。基本上,这是关于前一个模型输出的损失函数的梯度。
- 步骤4:分割节点 – XGBoost使用近似贪心算法(通常约3个近似带权重的分位数)来分割观测值的节点,这些分位数具有类似的权重总和。为了找到节点的分割值,它不考虑所有候选阈值,而是只使用该预测变量的分位数。
通过使用交叉验证和网格搜索可以确定最佳学习率。
XGBoost的简单Python实现
假设你有一个包含有关各种房屋和其价格的信息的数据集。数据集包括卧室数、浴室数、总面积、建筑年份等特征,并且你想要基于这些特征预测房屋的价格。
import xgboost as xgb# 初始化和训练XGBoost模型model_xgb = xgb.XGBRegressor(objective ='reg:squarederror', n_estimators = 100, seed = 42)model_xgb.fit(X_train, y_train)# 预测predictions = model_xgb.predict(X_test)# 评估模型mse = mean_squared_error(y_test, predictions)rmse = np.sqrt(mse)print(f"均方误差:{mse:.2f}")print(f"均方根误差:{rmse:.2f}")# 可视化:实际 vs 预测价格plt.scatter(y_test, predictions, color="forestgreen")plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=3)plt.xlabel('实际价格')plt.ylabel('预测价格')plt.title('XGBoost实际 vs 预测房价')plt.show()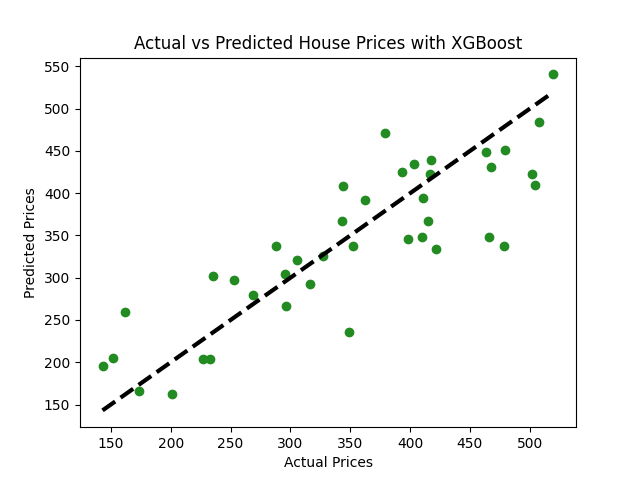

第三章:机器学习中的特征选择
构建有效的机器学习模型的路径通常涉及一个关键问题:我们应该包含哪些特征以生成可靠的预测,同时保持模型简单和可理解?这就是子集选择发挥重要作用的地方。
在机器学习中,我们通常处理大量特征,而并非所有特征都重要和信息丰富。将这些不相关的变量包括在模型中会导致机器学习模型的不必要复杂性,并影响模型的可解释性和性能。
通过去除这些不重要的变量,选择相对信息丰富的特征,我们可以得到一个更容易解释的模型,并且可能更准确。
让我们以一个具体的机器学习模型为例,以简化问题。
假设我们正在看一个多元线性回归模型(多个自变量和单个响应/因变量),而自变量有非常多。这个模型在解释方面可能会更加复杂。而且,由于其中一些特征可能不重要且对解释响应变量没有帮助,它可能导致不准确的预测。
在模型中选择重要变量的过程称为特征选择或变量选择。这个过程涉及到为我们认为与因变量相关的p个变量中的一个运行回归,并选择结果是性能最好或最差的模型。
有多种方法可以用于特征选择,通常分为以下三个类别:
- 子集选择(最佳子集选择,逐步特征选择)
- 正则化技术(L1 Lasso,L2 Ridge回归)
- 降维技术(PCA)
3.1 机器学习中的子集选择
机器学习中的子集选择是一种设计用于识别和使用一部分重要特征而省略其他特征的技术。这有助于创建更易解释的模型,并在某些情况下通过避免过拟合来更准确地预测。
在众多特征中进行选择时,有选择性地选择那些对预测模型有重大影响的特征变得非常重要。子集选择提供了一种系统方法来筛选预测变量的可能组合,目标是选择一个能够有效代表数据而不增加不必要复杂性的子集。
- 最佳子集选择:检查所有可能的组合并选择最优的一组预测变量。
- 逐步选择:逐步添加或删除预测变量,包括前向逐步选择和后向逐步选择。
- 随机子集选择:随机选择子集,引入模型选择的随机性因素。
在使用所有可用预测变量之间进行权衡时,存在着一种平衡:冒着模型过于复杂和潜在过拟合的风险,还是构建一个过于简单的模型可能会忽略重要的数据模式。
在本节中,我们将探讨这些子集选择技术。您将了解每种方法的工作原理以及对模型性能的影响,确保我们构建的模型是可靠、简单和有效的。
3.1.1 逐步特征选择技术
一种流行的子集选择技术是逐步特征选择技术。让我们看看两种不同的逐步特征选择方法:
- 前向逐步选择
- 后向逐步选择
前向逐步选择:前向逐步特征选择技术的做法是从仅包含截距的空模型开始。我们然后运行一系列简单回归,并选择具有最小残差平方和的模型变量。然后我们使用2个变量回归来做同样的事情,直到完成。
因此,前向逐步选择从不含预测变量的模型开始,然后逐个添加预测变量,直到所有的预测变量都在模型中。特别地,在每一步中,增加拟合度影响最大的变量被添加到模型中。
前向逐步选择可以总结如下:
步骤 1:让 M_0 为 null 模型,不包含任何特征。
步骤 2:对于 K = 0,…, p-1:
- 考虑包含 M_k 中的变量和一个额外特征或预测变量的所有模型(p-k 个模型)。
- 在这些 p-k 个模型中选择最佳模型,并用性能度量(如 RSS / R-squared)定义它为 M_(k+1)。
步骤 3:从 M_0,…, M_p 模型中选择表现最佳的单个模型(具有最小的交叉验证误差、Cp、AIC(Akaike信息准则)、BIC(贝叶斯信息准则)或调整的R-squared),作为最佳模型 M*。
因此,这个选择的理念是从简单开始,并增加模型中的预测变量数量。对于每个预测变量数量,考虑所有可能的变量组合并选择一个最佳模型:M_k。然后比较所有这些具有不同预测变量数目的模型(最佳 M_k),选择性能最佳的模型。
当 n < p 时,即当观察数大于线性回归的预测变量数时,可以使用此方法选择模型中的特征,以便首先使 LR 工作。
后向逐步特征选择:与前向逐步选择不同,后向逐步选择是从包含全部 p 个预测变量的完整模型开始的特征选择算法。然后选择带有 p 个预测变量的最佳模型。
因此,该模型逐个删除具有最大p值的变量,然后再选择最佳模型。
每次,重新拟合模型以确定最不显著的变量直到达到停止规则为止(例如,所有p值都需要小于5%)。然后,我们将这些具有不同预测变量数的模型(最佳M_ks)进行比较,并选择在这些M_0、…、M_p模型中表现最佳的单个模型(具有最小的交叉验证误差,C_p,AIC(赤池信息准则),BIC(贝叶斯信息准则)或调整的R-平方值是你的最佳模型M*)。
向后逐步特征选择可以总结如下:
第一步:令M_p为完整模型,包含所有特征。
第二步:对于k = p,p-1,…,1:
第三步:从这些M_0、…、M_p模型中选择在性能最佳的单个模型(具有最小的交叉验证误差,C_p,AIC(赤池信息准则),BIC(贝叶斯信息准则)或调整的R-平方值是你的最佳模型M*)。
与向前逐步选择相似,向后逐步特征选择技术只搜索(p+1)/2个模型,从而使其适用于p太大而无法应用其他选择技术的情况。
此外,向后逐步特征选择不一定能产生包含子集p个预测变量的最佳模型。它要求观测值或数据点n的数量大于模型变量p的数量,而向前逐步选择可在n < p的情况下使用。

3.2 机器学习中的正则化
正则化,也称为缩减,是解决机器学习模型过拟合问题的常用策略。
正则化的基本概念是故意引入一些偏差到模型中,从而显著降低模型的方差。
“缩减”一词源自该方法将一些估计的系数推向零,对它们进行惩罚,以防止它们过度提高模型的方差。
实践中有两种重要的正则化技术:岭回归,利用L2范数,和Lasso回归,利用L1范数。
3.2.1 岭回归(L2正则化)
让我们探索多元线性回归的例子,其中有pp个自变量或预测变量用于建模因变量yy。
值得记住,普通最小二乘(OLS)是一个广泛采用的估计技术,用于确定线性回归参数,前提是满足其假设。OLS通过最小化模型的残差平方和(RSS)来寻找最优系数。即:
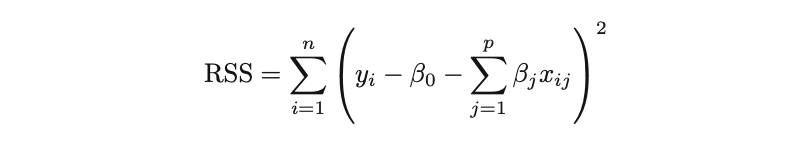
β 表示不同变量或预测器(X)的系数估计值。
岭回归(Ridge Regression)与最小二乘法(OLS)非常相似,唯一的区别在于系数估计通过最小化稍有不同的代价或损失函数来得到。即,岭回归系数估计 βˆR 的值使得最小化以下损失函数:
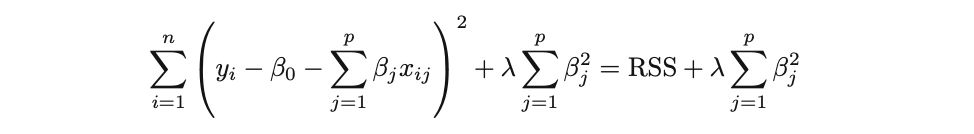
其中 λ(lambda,始终为正,≥ 0)是调谐参数或惩罚参数。从公式中可以看出,在岭回归的情况下,使用了 L2 惩罚或 L2 范数。
岭回归通过对某些变量施加惩罚,使它们的系数收缩至零,从而减小整体模型方差 – 但这些系数永远不会变为零。因此,模型参数从不设为确切的 0,这意味着模型的所有 p 个预测器仍然存在。
L2 范数(欧几里得距离)
L2 范数是线性代数中的数学术语。可以表示为:
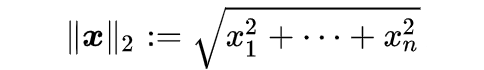
调谐参数 λ: 调谐参数 λ 用于控制惩罚对回归系数估计的相对影响。当 λ = 0 时,惩罚项没有影响,岭回归将产生普通最小二乘法的估计值。但当 λ → ∞(变得非常大)时,收缩惩罚的影响增加,岭回归系数估计趋近于 0。以下是此过程的可视化表示:
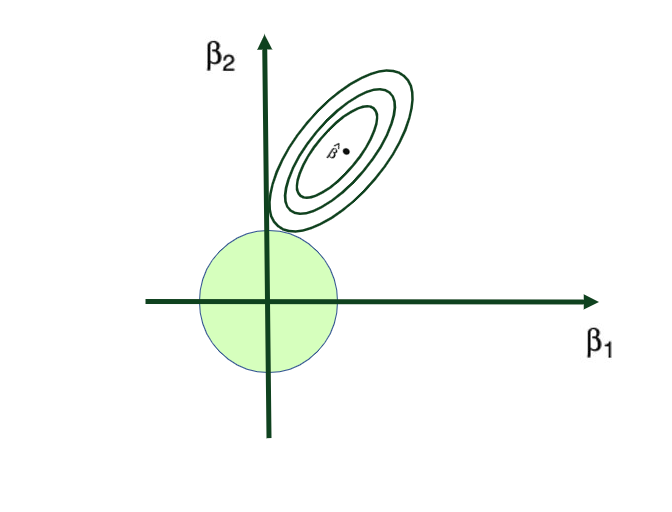
岭回归为什么有效?
岭回归相对普通最小二乘法的优势来自早期介绍的偏差-方差权衡现象。随着惩罚参数 λ 的增加,岭回归拟合的灵活性降低,使方差减小,但偏差增加。
3.2.2 Lasso 回归(L1 正则化)
Lasso 回归克服了岭回归的这个缺点。此处的 Lasso 回归系数估计 βˆλL 是最小化以下值得到的:
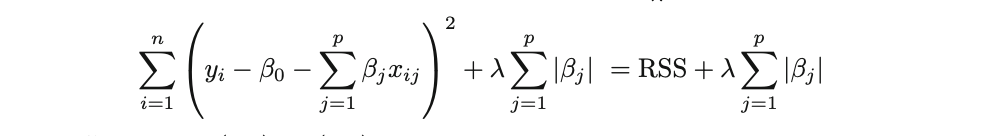
与岭回归类似,Lasso 将系数估计收缩至零。但是,在 Lasso 的情况下,使用了 L1 惩罚或 L1 范数,当调谐参数 λ 显著大时,某些系数估计强制等于零。
因此,像许多特征选择技术一样,Lasso 回归除了解决过拟合问题外,还执行了变量选择。
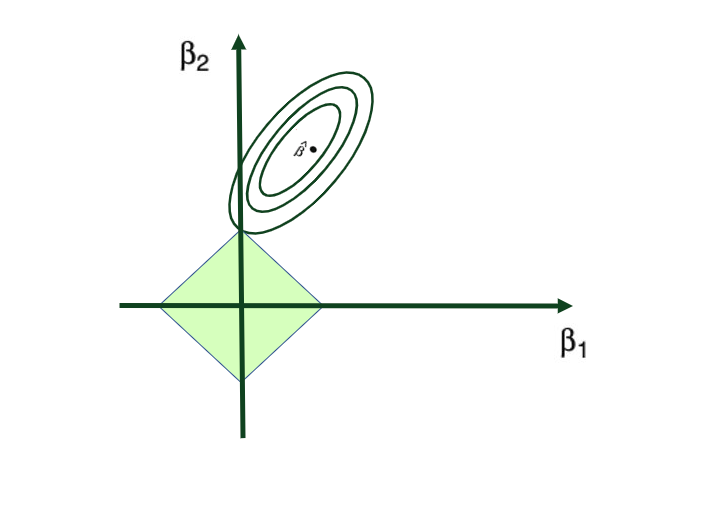
L1 范数(曼哈顿距离)
L1 范数是线性代数中的数学术语。可以表示为:
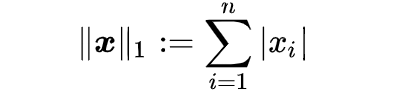
Lasso 回归为什么有效?
与岭回归类似,Lasso 回归相对于普通最小二乘法的优势来自早期介绍的偏差-方差权衡。随着 λ 的增加,岭回归拟合的灵活性减少,导致方差减小但偏差增加。此外,Lasso 还执行特征选择。
3.2.3 Lasso vs 岭回归
Lasso 回归将系数估计收缩至零,甚至在调谐参数 λ 显著大时,强制某些系数完全等于零。因此,像许多特征选择技术一样,Lasso 回归在解决过拟合问题之外还执行了变量选择。
将岭回归(Ridge Regression)和Lasso回归(Lasso Regression)进行比较时,将两个早期的图形放在一起就能很清楚地看出两者的区别:
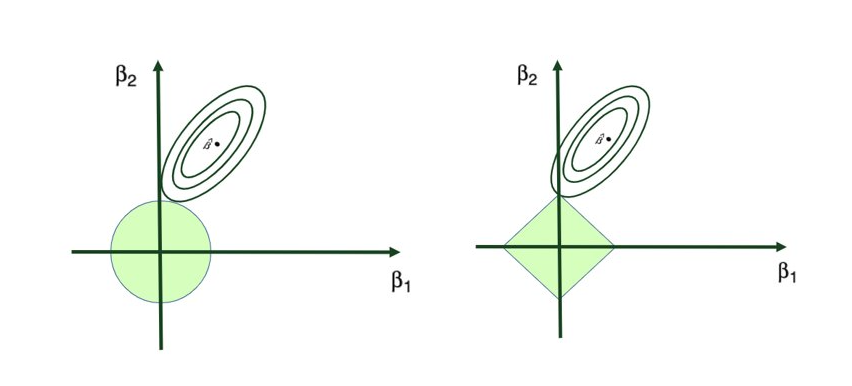
如果你想详细了解正则化技术,请阅读这篇教程:
 Tatev Karen AslanyanTowards Data Science
Tatev Karen AslanyanTowards Data Science
第4章:机器学习中的重采样技术
当我们只有训练数据并且希望对模型在未知数据上的性能做出判断时,我们可以使用重采样技术来创建人工测试数据。
重采样技术通常分为两类:交叉验证(Cross-Validation)和自助法(Bootstrapping)。它们通常用于以下三个目的:
- 模型评估:评估模型性能(计算测试错误率)
- 模型方差:计算模型的方差以检查模型的泛化能力
- 模型选择:选择模型的灵活性
例如,为了估计线性回归拟合的可变性,我们可以从训练数据中重复抽取不同的样本,对每个新样本进行线性回归拟合,然后观察所得拟合的差异程度。
4.1 交叉验证(Cross-Validation)
交叉验证可以用于估计与给定统计学习方法相关的测试误差,以进行:
- 模型评估:通过计算测试错误率来评估模型的性能
- 模型选择:选择适当的灵活性级别
将一部分训练观测数据从拟合过程中分离出来,然后将统计学习方法应用于这些分离出来的观测数据。
交叉验证通常分为以下三种类型:
- 验证集法
- K折交叉验证(K-fold CV)
- 留一交叉验证(LOOCV)
4.1.1 验证集法
这是一种简单的方法,将数据随机分成训练集和验证集。这种方法通常使用Sklearn的train_test_split()函数。
然后,用训练数据(通常为数据的80%)训练模型,并用其预测留出或验证集(通常为数据的20%)的值,以计算测试错误率。
4.1.2 留一交叉验证(LOOCV)
留一交叉验证与验证集法类似。但每次它都从训练集中留出一个观测数据,并使用剩下的n-1个观测数据来训练模型,并计算该预测的均方误差(MSE)。因此,在LOOCV的情况下,模型需要拟合n次(其中n是模型中的观测数)。
然后,对所有观测数据重复此过程,并计算n次MSE。MSE的均值是交叉验证错误率,可以表示如下:
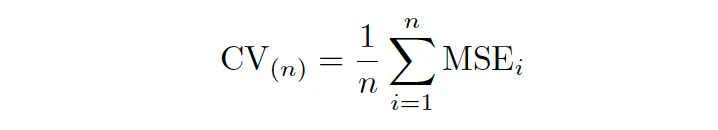
4.1.3 K折交叉验证(K-ford CV)
K-Fold CV是验证集方法(高方差和高偏差,但计算效率高)与LOOCV(低偏差和低方差,但计算效率低)之间的乌云中的银边。
在K-Fold CV中,数据随机样本分为K个大小相等的样本(K折)。然后,每次都使用1作为验证数据,其余作为训练数据,模型被拟合K次。 K个MSE的均值形成交叉验证测试误差率。
请注意,LOOCV是K折CV的特殊情况,其中K = N,并可以表示如下:
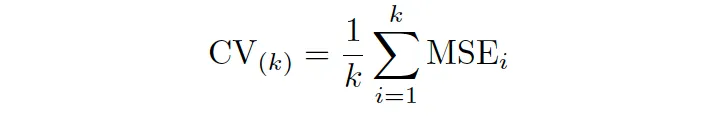
4.2 在K-Fold CV中选择最佳k值
K-Fold中k的选择是偏差-方差权衡和模型效率的问题。通常,K-Fold CV和LOOCV提供类似的结果,并且它们的性能可以使用模拟数据进行评估。
但是,与K-Fold CV相比,LOOCV具有较低的偏差(无偏) ,因为LOOCV使用的训练数据比K-Fold CV多。但是LOOCV的方差比K-Fold CV大,因为LOOCV对于每个项目都在几乎相同的数据上拟合模型,并且结果与K-Fold的结果相比高度相关。
由于高度相关结果的均值比较低度相关结果的均值具有更高的方差,因此LOOCV的方差更高。
- K = N(LOOCV),K越大→方差越大,偏差越小
- K = 1,K越小→方差越小,偏差越大
考虑到这些信息,我们可以计算模型在不同K值(比如K = 3,5,6,7… 10)或分类模型的一型、二型和总体模型分类误差的性能。然后,表现最佳的模型的K可以是使用ROC曲线(分类情况)或拐点法(回归情况)的最佳K。

4.3 自助法
自助法是另一种非常流行的重抽样技术,用于各种目的。其中之一是有效地估计估计/模型的可变性,或者从现有样本中创建人造样本并改善模型性能(如装袋或随机森林的情况)。
在许多情况下,直接计算感兴趣数量的标准偏差很困难甚至不可能,因此使用自助法。
- 它是一种非常有用的方法,用于量化与统计学习方法相关的不确定性并获取标准错误/可变性的指标。
- 对于线性回归没有用,因为标准R / Python提供这些结果(系数的SE)。
自助法对于其他方法也非常方便,其中可变性更难以量化。自助抽样是有替换地进行的,这意味着同一观察可以在自助数据集中出现多次。
因此,自助法通过替换从原始训练样本中重新采样,从而得到B个不同的样本。然后,对于这些模拟样本中的每一个,计算系数估计。然后,通过取这些系数估计的均值并使用常用的SE公式,计算自助模型的标准错误。
在这里阅读更多信息。
第5章:优化技术
了解机器学习模型的基础知识并学习如何训练这些模型绝对是成为技术数据科学家的重要部分。但这只是工作的一部分。
为了使用机器学习模型解决业务问题,您需要在建立基准之后对其进行优化。也就是说,您需要优化机器学习模型中的超参数集,以找到导致性能最佳的模型的一组最佳参数(其他条件相同)。
因此,要优化或调整您的机器学习模型,您需要执行超参数优化。通过找到超参数值的最佳组合,我们可以减小模型产生的错误并构建最准确的模型。
模型超参数是模型中的常数。它是模型外部的,并且其值无法从数据中估计(而应该在模型训练之前事先指定)。例如,kNN(k-最近邻算法)中的k或神经网络中的隐藏层数量。
超参数优化方法通常可以分为以下几类:
- 穷举搜索或蛮力算法(如网格搜索)
- 梯度下降(批量梯度下降、随机梯度下降、带动量的随机梯度下降、Adam)
- 遗传算法
在本手册中,我只将讨论前两种优化技术。
5.1 蛮力算法(网格搜索)
穷举搜索(通常称为网格搜索或蛮力算法)是通过检查每个超参数候选项并计算模型错误率来寻找最佳超参数的过程。
一旦我们为每个超参数创建可能值的列表,对于每个可能的超参数值组合,我们计算模型错误率并将其与当前最佳模型(具有最小错误率的模型)进行比较。在每次迭代中,如果新的参数值导致较低的错误率,则更新最佳模型。
优化方法很简单。例如,如果您正在使用K-means聚类算法,您可以手动搜索正确的聚类数。但如果有数百或数千个可能的超参数值组合需要考虑,模型可能需要数小时或数天进行训练 – 并且变得非常繁重和缓慢。因此,大多数情况下,蛮力搜索是低效的。
要优化或调整您的机器学习模型,您需要执行超参数优化。通过找到超参数值的最佳组合,我们可以减小模型产生的误差并构建最准确的模型。
当涉及到梯度下降类型的优化技术时,各种变体,如批量梯度下降、随机梯度下降等,在使用数据计算损失函数的梯度方面存在差异。
让我们通过J(θ)定义这个损失函数,其中θ(theta)代表我们要优化的参数。
数据使用量是在调整参数的准确性和执行此类调整所需时间之间的权衡。换句话说,我们使用的数据样本越大,我们可以期望参数的调整更准确,但是该过程将会变得更加缓慢。
相反,也成立。数据样本越小,参数调整的准确性就越低,但是过程会更快。
5.2 梯度下降优化(GD)
批量梯度下降算法(通常简称为梯度下降或GD)使用整个训练数据计算损失函数J(θ)相对于目标参数的梯度。
我们首先在每次迭代中预测每个观察值的值,并将其与训练数据中给定的值进行比较。这两个值用于计算每个观察值的预测误差项,然后用于更新模型参数。此过程持续进行,直到模型收敛。
损失函数的梯度或一阶导数可以表示如下:
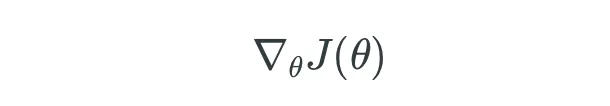
然后,这个梯度用于更新目标参数的前一次迭代值。即:
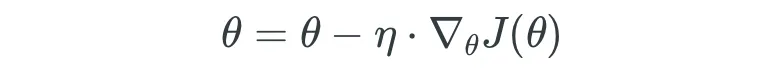
其中:
- θ:表示您要优化的模型参数或权重。在许多情况下,特别是在神经网络中,θ可以是包含许多单独权重的向量。
- η:这是学习率。它是一个超参数,指定每次迭代在朝向成本函数最小值的方向上的步长大小。较小的学习率可能使优化更精确,但可能也会减慢收敛过程,而较大的学习率可能加快收敛但可能会超过最小值。可以是[0,1]之间的值,但通常是介于(0.001和0.04)之间的数。
- ∇J(θ):这是损失函数J相对于参数θ的梯度。它指示J最陡增加的方向和大小。通过将其与当前参数值相减(乘以学习率),我们沿着J最陡减小的方向调整θ。
有两个主要的缺点使得GD这个优化技术在处理大规模和复杂数据集时不太受欢迎。因为在每次迭代中都需要使用和存储整个训练数据,计算时间可能非常长,导致进程非常缓慢。除此之外,存储如此大量的数据会导致内存问题,使得GD计算量大而缓慢。

5.3 随机梯度下降(SGD)
随机梯度下降(SGD)方法,也被称为增量梯度下降,是一种用于解决带有微分目标函数的优化问题的迭代方法,与GD完全相同。
但是与GD不同,SGD不会使用整个训练数据集来更新参数值。SGD方法通常被称为梯度下降的随机逼近,旨在找到包含无法直接估计的参数的随机模型的极值点或零点。
SGD通过在训练数据集中扫过数据并在每次迭代中更新参数值来最小化此成本函数。
在SGD中,所有模型参数在每个迭代步骤中都会得到改进,而只有一个训练样本。因此,SGD的算法通过查看一个单独且随机抽样的训练集(因此称为随机)来改进参数,而不是一次性遍历所有训练样本来修改模型参数。即:
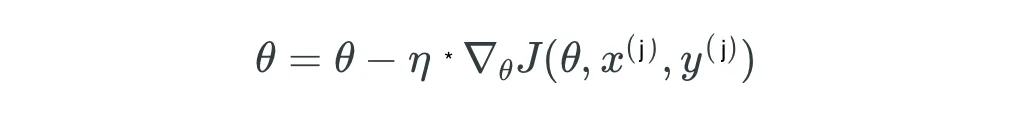
其中
- θ:代表您尝试优化的模型的参数或权重。在许多上下文中,特别是在神经网络中,θ可以是包含许多个体权重的向量。
- η:学习率。这是一个超参数,在每次迭代中移动到损失函数的最小值时确定步长的大小。较小的学习率可能使优化更精确,但也可能减慢收敛过程,而较大的学习率可能加快收敛,但可能导致超过最小值。
- ∇J(θ,x(i),y(i)):对于给定的输入x(i)和对应的目标输出y(i),这是成本函数J相对于参数θ的梯度。它指示J最陡增加的方向和大小。通过从当前参数值中减去这个值(乘以学习率),我们将θ调整到J最陡减少的方向。
- x(i):表示数据集中的第i个输入数据样本。
- y(i):是第i个输入数据样本的真实目标输出。
在随机梯度下降(SGD)的背景下,更新规则适用于单个数据样本x(i)和y(i),而不是整个数据集,这将是批量梯度下降的情况。
这一步使得寻找优化问题的全局最小值的过程加速,这是SGD与GD的不同之处。因此,SGD持续调整参数,试图朝着目标函数的全局最小值的方向移动。
SGD解决了GD计算时间缓慢的问题,因为它能够很好地适应大数据和模型的大小。但是,虽然SGD方法本身简单快速,但它被称为“糟糕的优化器”,因为它容易找到局部最优解而不是全局最优解。
在SGD中,每次迭代步骤中都改进所有模型参数,只使用一个训练样本。因此,SGD通过查看单个训练样本来改进参数。
这一步使得寻找优化问题的全局最小值的过程加速。这是SGD与GD的不同之处。

5.4 带动量的SGD
当误差函数复杂且非凸时,SGD算法通常会朝着众多局部最小值的方向错误地移动,而不是找到全局最优解。这会导致更长的计算时间。
为了解决这个问题并进一步改进SGD算法,引入了各种方法。一种流行的逃离局部最小值并朝着全局最小值方向移动的方法是带冲量的SGD。
带冲量的SGD方法的目标是加快梯度向量在全局最小值方向上的加速度,从而实现更快的收敛。
冲量背后的思想是模型参数通过使用先前参数调整的方向和值来学习。此外,调整值是根据近期调整的权重来计算,前期调整的权重较小。
之所以存在这种差异,是因为在SGD方法中,我们没有确定损失函数的精确导数,而是在一个小批次上进行估计。由于梯度是有噪声的,它很可能不总是朝着最优方向移动。
冲量有助于更准确地估计这些导数,从而在朝着全局最小值的过程中做出更好的方向选择。
经典SGD和带冲量的SGD性能差异的另一个原因在于病态曲率区域,也称为峡谷区域。
峡谷区域可以用下图表示。橙色线表示基于梯度的方法的路径,而深蓝色线表示理想路径,指向结束全局最优方向。
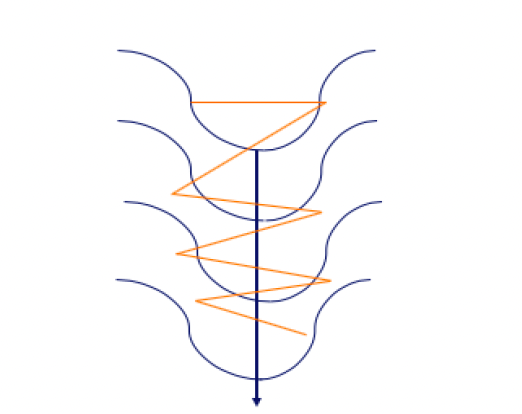
为了了解SGD和带冲量的SGD之间的差异,让我们看一下下面的图。

左侧是不带冲量的SGD方法。右侧是带冲量的SGD方法。橙色图案表示梯度在搜索全局最小值时的路径。
冲量背后的思想是模型参数通过使用先前参数调整的方向和值来学习。此外,调整值是根据近期调整的权重来计算,前期调整的权重较小。

5.5 Adam优化器
另一种增强SGD优化过程的流行技术是由Kingma和Ba(2015)引入的自适应矩估计(Adam)。Adam是带有冲量方法的扩展版本。
与使用相同学习率的所有参数更新的带冲量SGD相比,Adam算法为不同的参数定义了不同的学习率。
该算法根据梯度的一阶和二阶导数(损失函数的一阶和二阶导数的估计值)的估计值,为每个参数计算独立的自适应学习率。
因此,每个参数都有一个独特的学习率,该学习率使用渐衰平均值来更新梯度的第一和第二阶矩估计(均值和方差)。

主要观点和下一步
在本手册中,我们涵盖了机器学习的基础知识和更多知识。从基础知识到高级技术,我们解析了全球技术中广泛使用的流行机器学习算法和支持它们的关键优化方法。
在了解每个概念的过程中,我们看到了一些实际示例和Python代码,确保您不仅理解理论,还理解其应用。
您的机器学习之旅还在继续,本指南是您的参考资料。这不是一次性阅读 – 它是您在这个领域中进展和发展时可以回顾的资源。凭借这些知识,您已经准备好在高水平上自信地应对大多数实际机器学习挑战。但这只是个开始。
关于作者 — 那就是我!
我是Tatev,高级机器学习和人工智能研究员。我有幸在包括美国、英国、加拿大和荷兰在内的多个国家从事数据科学工作。
拥有经济计量学的硕士和学士学位,我的机器学习和人工智能之旅简直令人难以置信。在本科和硕士期间,我从我的技术研究中汲取了丰富的知识,并在数据科学行业拥有超过5年的实践经验。下面是我整理出的机器学习主题的高级总结,与大家分享。
如何深入学习?
在学习了本指南后,如果你渴望更深入地学习,并且结构化学习适合你,考虑加入我们在LunarTech的课程。跟随课程《基础到机器学习》,这是一个全面的计划,提供深入理解理论、实践实施、丰富的练习材料和量身定制的面试准备,帮助你成功地迈入你自己的阶段。
这门课程也是终极数据科学训练营的一部分,该训练营已被评为2023年最佳数据科学训练营之一,并被Forbes、Yahoo、Entrepreneur等杂志评选为特色训练营。这是你参与一个以创新和知识为核心的社区的机会。你可以在LunarTech报名参加终极数据科学训练营免费试听。
 AJ Ignacio – 品牌撰稿人Forbes Australia
AJ Ignacio – 品牌撰稿人Forbes Australia
 Anne SchulzeEntrepreneur Georgia
Anne SchulzeEntrepreneur Georgia
 Newsfile Corp.Yahoo Finance
Newsfile Corp.Yahoo Finance
与我联系:

 Tatev Karen数据科学和人工智能新闻通讯
Tatev Karen数据科学和人工智能新闻通讯
想要了解关于数据科学、机器学习和人工智能职业的一切,并学习如何获得数据科学工作吗?下载这个免费的数据科学和人工智能职业手册
感谢您选择这篇指南作为您的学习伴侣。在您继续探索广阔的机器学习领域时,我希望您能以自信、精确和创新的精神前行。祝愿您在未来的所有努力中一切顺利!


Leave a Reply